题目内容
矩形ABCD的对角线AC、BD相交于点M (2,0),AB边所在直线的方程为:x-3y-6=0.若点N(1,-5)在直线AD上.
(1)求点A的坐标及矩形ABCD外接圆的方程;
(2)过直线x-y+4=0上一点P作(1)中所求圆的切线,设切点为E、F,求四边形PEMF面积的最小值.
解:(1)∵AB边所在直线的方程为:x-3y-6=0,∴且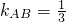 ,
,
∵A B⊥AD,∴kAD=-3
∵点N(1,-5)在直线AD上
∴直线AD的方程为:y+5=-3(x-1)即3x+y+2=0 …1分
由 ,解得
,解得
即A(0,-2)…3分
∵ABCD是矩形,∴ABCD外接圆的圆心为对角线AC与BD的交点,即M(2,0),
半径r=|AM|=2.故其方程为(x-2)2+y2=8…6分
(2)由切线的性质知:四边形PEMF的面积S=|PE|•r=r =
= …9分
…9分
∴四边形PEMF的面积取最小值时,|PM|最小,即为圆心M到直线x-y+4=0的距离d=3.…11分
∴四边形PEMF的面积S的最小值 .…12分
.…12分
分析:(1)先求直线AD的方程,再与AB的方程联立,即可求得点A的坐标;ABCD外接圆的圆心为对角线AC与BD的交点,半径r=|AM|=2,由此可得结论;
(2)先表示出四边形PEMF面积,再转化为求圆心到直线的距离即可.
点评:本题考查直线方程、圆的标准方程,考查四边形面积的求解,考查学生分析解决问题的能力,正确表示四边形PEMF的面积是关键.
 ,
,∵A B⊥AD,∴kAD=-3
∵点N(1,-5)在直线AD上
∴直线AD的方程为:y+5=-3(x-1)即3x+y+2=0 …1分
由
 ,解得
,解得
即A(0,-2)…3分
∵ABCD是矩形,∴ABCD外接圆的圆心为对角线AC与BD的交点,即M(2,0),
半径r=|AM|=2.故其方程为(x-2)2+y2=8…6分
(2)由切线的性质知:四边形PEMF的面积S=|PE|•r=r
 =
= …9分
…9分∴四边形PEMF的面积取最小值时,|PM|最小,即为圆心M到直线x-y+4=0的距离d=3.…11分
∴四边形PEMF的面积S的最小值
 .…12分
.…12分分析:(1)先求直线AD的方程,再与AB的方程联立,即可求得点A的坐标;ABCD外接圆的圆心为对角线AC与BD的交点,半径r=|AM|=2,由此可得结论;
(2)先表示出四边形PEMF面积,再转化为求圆心到直线的距离即可.
点评:本题考查直线方程、圆的标准方程,考查四边形面积的求解,考查学生分析解决问题的能力,正确表示四边形PEMF的面积是关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
 如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,△ABF、△CDE是等边三角形,CD=1,EF=
如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,△ABF、△CDE是等边三角形,CD=1,EF=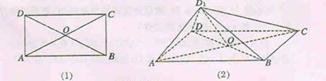
 在多面体ABCDEF中,点O是矩形ABCD的对角线的交点,平面CDE是等边三角形,棱EF∥BC且EF=
在多面体ABCDEF中,点O是矩形ABCD的对角线的交点,平面CDE是等边三角形,棱EF∥BC且EF= 如图所示,矩形ABCD的对角线交于点G,AD⊥平面ABE,AE=
如图所示,矩形ABCD的对角线交于点G,AD⊥平面ABE,AE=