题目内容
直角三角形的斜边长为m,则其内切圆半径的最大值为( )A.
m B.
m C.
m D.(
-1)m
解析:设两直角边分别为a、b,内切圆半径为r,
则a2+b2=m2.∵a2+b2≥,∴m2≥.∴a+b≤m.
∵r=,∴rmax=
m.
答案:B
练习册系列答案
相关题目
如图，一个空间几何体的正视图、侧视图、俯视图均为全等的等腰直角三角形，如果直角三角形的斜边长为2| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
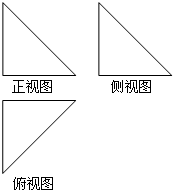（2012•北京模拟）如图，一个空间几何体的正视图（或称主视图）、侧视图（或称左视图）、俯视图均为全等的等腰直角三角形，如果直角三角形的斜边长为