题目内容
 已知数列{an}中,an=n(n∈N+),把它的各项依次排列如图所示的三角形状,第一行1项,第二行3项,…第一行 a1
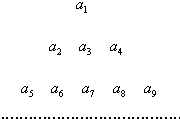
已知数列{an}中,an=n(n∈N+),把它的各项依次排列如图所示的三角形状,第一行1项,第二行3项,…第一行 a1每行依次比上一行多两项,第二行 a2,a3,a4,若a2012被排在第S行第t项(从左往右)的位置,第三行 a5,a6,a7,a8,a9
则S=
45
45
t=76
76
.…分析:观察图形,得到规律:第m行的最后一个数是am2,第m行中有2m-1项,由442=1936,452=2025,知第45行的第一项为a1937,由此能求出结果.
解答:解:由题意知第一行的最后一个数字是a1,第二行的最后一个数字是a4,第三行的最后一个数字是a9,
∴第m行的最后一个数是am2,
∵442=1936,452=2025,
∴a2012被排在第45行,
∵第一行中有2×1-1=1项,
第二行中有2×2-1=3项,
第三行中有2×3-1=5项,
∴第m行中有2m-1项,
∴第45行中有89项,
∵第45行中的第89项为a2025,第44行的最后一项为a1936,
∴第45行的第一项为a1937,
∴a2012是第45行的第76年元素.
故答案为:45,76.
∴第m行的最后一个数是am2,
∵442=1936,452=2025,
∴a2012被排在第45行,
∵第一行中有2×1-1=1项,
第二行中有2×2-1=3项,
第三行中有2×3-1=5项,
∴第m行中有2m-1项,
∴第45行中有89项,
∵第45行中的第89项为a2025,第44行的最后一项为a1936,
∴第45行的第一项为a1937,
∴a2012是第45行的第76年元素.
故答案为:45,76.
点评:本题考查数列中元素的位置的判断,解题时要认真审题,仔细观察,注意总结规律,合理地进行等价转化.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|