题目内容
已知函数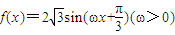 .
.(1)若
 是最小正周期为π的偶函数,求ω和θ的值;
是最小正周期为π的偶函数,求ω和θ的值;(2)若g(x)=f(3x)在
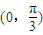 上是增函数,求ω的最大值;并求此时f(x)在[0,π]上的取值范围.
上是增函数,求ω的最大值;并求此时f(x)在[0,π]上的取值范围.
【答案】分析:(1)由f(x+θ)=2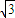 sin(ωx+ωθ+
sin(ωx+ωθ+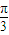 )(0<θ<
)(0<θ< )是最小正周期为π的偶函数,利用周期公式与诱导公式即可求得ω和θ的值;
)是最小正周期为π的偶函数,利用周期公式与诱导公式即可求得ω和θ的值;
(2)g(x)=f(3x)=2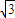 sin(3ωx+
sin(3ωx+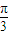 ),利用正弦函数的单调性可求ω的最大值;并求此时f(x)在[0,π]上的取值范围.
),利用正弦函数的单调性可求ω的最大值;并求此时f(x)在[0,π]上的取值范围.
解答:解:(1)∵f(x)=2 sin(ωx+
sin(ωx+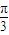 )(0<θ<
)(0<θ<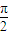 ),
),
∴f(x+θ)=2 sin(ωx+ωθ+
sin(ωx+ωθ+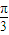 )(0<θ<
)(0<θ<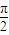 ),
),
又f(x+θ)是最小正周期为π的偶函数,
∴ω=2,
∴2θ+ =kπ+
=kπ+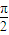 ,(k∈Z),又0<θ<
,(k∈Z),又0<θ< ,
,
∴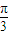 <2θ+
<2θ+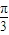 <
<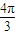 .
.
∴k=0,θ= .
.
(2)∵g(x)=f(3x)=2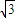 sin(3ωx+
sin(3ωx+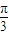 )在(0,
)在(0, )上是增函数,
)上是增函数,
∴由2kπ- ≤3ωx+
≤3ωx+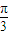 ≤2kπ+
≤2kπ+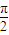 (k∈Z),ω>0得:
(k∈Z),ω>0得:
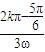 ≤x≤
≤x≤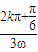 (k∈Z),
(k∈Z),
∵f(3x)=2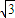 sin(3ωx+
sin(3ωx+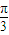 )在(0,
)在(0,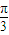 )上是增函数,
)上是增函数,
∴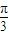 ≤
≤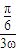 ,
,
∴0<ω≤ .
.
∴ωmax= .
.
当ω= 时,f(x)=2
时,f(x)=2 sin(
sin( x+
x+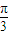 ).
).
∵x∈[0,π],
∴ x+
x+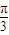 ∈[
∈[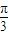 ,
,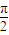 ],
],
∴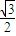 ≤sin(
≤sin( x+
x+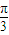 )≤1.
)≤1.
∴3≤2 sin(
sin( x+
x+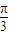 )≤2
)≤2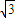 .
.
∴当x∈[0,π],f(x)=2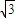 sin(
sin( x+
x+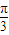 )∈[3,2
)∈[3,2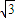 ].
].
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查正弦函数的周期与单调性,考查三角综合运算能力,属于中档题.
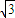 sin(ωx+ωθ+
sin(ωx+ωθ+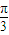 )(0<θ<
)(0<θ< )是最小正周期为π的偶函数,利用周期公式与诱导公式即可求得ω和θ的值;
)是最小正周期为π的偶函数,利用周期公式与诱导公式即可求得ω和θ的值;(2)g(x)=f(3x)=2
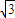 sin(3ωx+
sin(3ωx+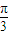 ),利用正弦函数的单调性可求ω的最大值;并求此时f(x)在[0,π]上的取值范围.
),利用正弦函数的单调性可求ω的最大值;并求此时f(x)在[0,π]上的取值范围.解答:解:(1)∵f(x)=2
 sin(ωx+
sin(ωx+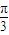 )(0<θ<
)(0<θ<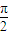 ),
),∴f(x+θ)=2
 sin(ωx+ωθ+
sin(ωx+ωθ+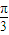 )(0<θ<
)(0<θ<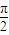 ),
),又f(x+θ)是最小正周期为π的偶函数,
∴ω=2,
∴2θ+
 =kπ+
=kπ+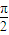 ,(k∈Z),又0<θ<
,(k∈Z),又0<θ< ,
,∴
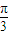 <2θ+
<2θ+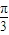 <
<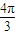 .
.∴k=0,θ=
 .
.(2)∵g(x)=f(3x)=2
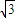 sin(3ωx+
sin(3ωx+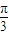 )在(0,
)在(0, )上是增函数,
)上是增函数,∴由2kπ-
 ≤3ωx+
≤3ωx+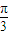 ≤2kπ+
≤2kπ+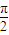 (k∈Z),ω>0得:
(k∈Z),ω>0得: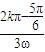 ≤x≤
≤x≤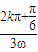 (k∈Z),
(k∈Z),∵f(3x)=2
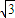 sin(3ωx+
sin(3ωx+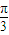 )在(0,
)在(0,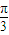 )上是增函数,
)上是增函数,∴
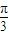 ≤
≤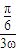 ,
,∴0<ω≤
 .
.∴ωmax=
 .
.当ω=
 时,f(x)=2
时,f(x)=2 sin(
sin( x+
x+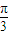 ).
).∵x∈[0,π],
∴
 x+
x+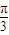 ∈[
∈[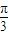 ,
,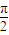 ],
],∴
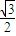 ≤sin(
≤sin( x+
x+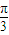 )≤1.
)≤1.∴3≤2
 sin(
sin( x+
x+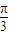 )≤2
)≤2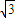 .
.∴当x∈[0,π],f(x)=2
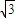 sin(
sin( x+
x+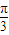 )∈[3,2
)∈[3,2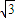 ].
].点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查正弦函数的周期与单调性,考查三角综合运算能力,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 ,
,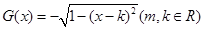
 是常数,问当
是常数,问当 有最大值,并求出
有最大值,并求出 的值;
的值; 同时满足条件:(甲)
同时满足条件:(甲) 取最小值的
取最小值的 ?
? ,求使
,求使 的
的 的取值范围.
的取值范围.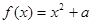 .
.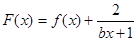 是偶函数,在定义域上
是偶函数,在定义域上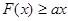 恒成立,求实数
恒成立,求实数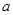 的取值范围;
的取值范围;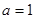 时,令
时,令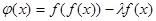 ,问是否存在实数
,问是否存在实数 ,使
,使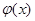 在
在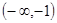 上是减函数,在
上是减函数,在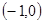 上是增函数?如果存在,求出
上是增函数?如果存在,求出 ,
,
 是偶函数,求
是偶函数,求 的值。
的值。 ,
, ,求
,求 的最小值。
的最小值。 ,
, 是
是 的极值点,求
的极值点,求 值;
值; 上是增函数,求实数
上是增函数,求实数