题目内容
20.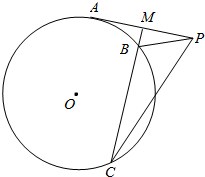 自⊙O外一点p引切线与⊙O切于点A,M为PA的中点,过M引割线交⊙O于B、C两点.
自⊙O外一点p引切线与⊙O切于点A,M为PA的中点,过M引割线交⊙O于B、C两点.求证:
(Ⅰ)PM2=MB•MC;
(Ⅱ)∠MCP=∠MPB.
分析 (Ⅰ)根据切割线定理,得到AM是MB和MC的比例中项,结合AM=MP即可证明PM2=MB•MC;
(Ⅱ)由MP2=MB•MC得$\frac{PM}{MC}=\frac{MB}{PM}$,再结合公共角∠BMP=∠PMC,得三角形BMP与三角形PMC相似,从而得到对应角相等,命题得证.
解答 证明:(Ⅰ)∵AM切圆于点A
∴AM2=MB•MC
又∵M为PA中点,AM=MP
∴MP2=MB•MC;
(Ⅱ)∵MP2=MB•MC,
∴$\frac{PM}{MC}=\frac{MB}{PM}$,
又∵∠BMP=∠PMC
∴△BMP∽△PMC(边角边)
∴∠MCP=∠MPB.
点评 本题考查了圆当中的比例线段,以及三角形相似的有关知识点,属于中档题.找到题中的相似三角形来证明角的相等,是解决本题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
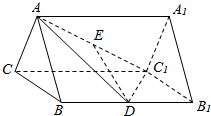 在三棱柱ABC-A1B1C1中,△ABC是边长为2的正三角形,侧面BB1C1C是矩形,D、E分别是线段BB1、AC1的中点.
在三棱柱ABC-A1B1C1中,△ABC是边长为2的正三角形,侧面BB1C1C是矩形,D、E分别是线段BB1、AC1的中点.
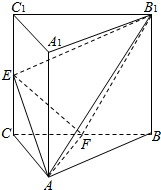 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,E,F分别是CC1,BC的中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,E,F分别是CC1,BC的中点.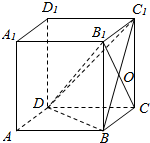 如图,边长为2的正方体ABCD-A1B1C1D1中,B1C与BC1相交于点O.
如图,边长为2的正方体ABCD-A1B1C1D1中,B1C与BC1相交于点O.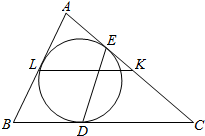 如图,己知L、K分别是△ABC的边AB、AC的中点.△ABC的内切圆⊙l分别与边BC、CA切于点D、E.求证:KL、DE的交点在∠ABC的角平分线上.
如图,己知L、K分别是△ABC的边AB、AC的中点.△ABC的内切圆⊙l分别与边BC、CA切于点D、E.求证:KL、DE的交点在∠ABC的角平分线上.