题目内容
等轴双曲线C与椭圆
+
=1有公共的焦点,则双曲线C的方程为
-
=1
-
=1.
| x2 |
| 10 |
| y2 |
| 6 |
| x2 |
| 2 |
| y2 |
| 2 |
| x2 |
| 2 |
| y2 |
| 2 |
分析:设出双曲线的方程,求出椭圆的焦点坐标,利用等轴双曲线C与椭圆
+
=1有公共的焦点,即可求得双曲线C的方程.
| x2 |
| 10 |
| y2 |
| 6 |
解答:解:设双曲线的方程为
-
=1,椭圆的焦点坐标为F1(-2,0),F2(2,0).
∵等轴双曲线C与椭圆
+
=1有公共的焦点,
∴a2+a2=22=4,所以a2=2.
所以双曲线C的方程为
-
=1.
故答案为:
-
=1
| x2 |
| a2 |
| y2 |
| a2 |
∵等轴双曲线C与椭圆
| x2 |
| 10 |
| y2 |
| 6 |
∴a2+a2=22=4,所以a2=2.
所以双曲线C的方程为
| x2 |
| 2 |
| y2 |
| 2 |
故答案为:
| x2 |
| 2 |
| y2 |
| 2 |
点评:本题考查椭圆的性质,考查双曲线的标准方程,确定几何量之间的关系是关键.

练习册系列答案
相关题目
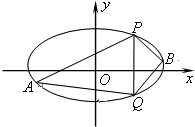 已知中心在坐标原点,坐标轴为对称轴的椭圆C和等轴双曲线C1,点
已知中心在坐标原点,坐标轴为对称轴的椭圆C和等轴双曲线C1,点
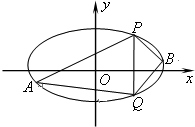 已知中心在坐标原点,坐标轴为对称轴的椭圆C和等轴双曲线C1,点
已知中心在坐标原点,坐标轴为对称轴的椭圆C和等轴双曲线C1,点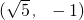 在曲线C1上,椭圆C的焦点是双曲线C1的顶点,且椭圆C与y轴正半轴的交点M到直线
在曲线C1上,椭圆C的焦点是双曲线C1的顶点,且椭圆C与y轴正半轴的交点M到直线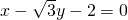 的距离为4.
的距离为4. ,求四边形APBQ面积的最大值.
,求四边形APBQ面积的最大值.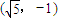 在曲线C1上,椭圆C的焦点是双曲线C1的顶点,且椭圆C与y轴正半轴的交点M到直线
在曲线C1上,椭圆C的焦点是双曲线C1的顶点,且椭圆C与y轴正半轴的交点M到直线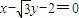 的距离为4.
的距离为4. ,求四边形APBQ面积的最大值.
,求四边形APBQ面积的最大值.