题目内容
函数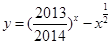 的零点的个数为( )
的零点的个数为( )
A. | B. | C. | D. |
C
解析试题分析:函数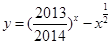 的零点的个数,即
的零点的个数,即 根的个数,也就是
根的个数,也就是 和
和 两个图像的交点个数,
两个图像的交点个数, 在R上单调递减,且横过点
在R上单调递减,且横过点 。
。 在
在 单调递增,起点为
单调递增,起点为 ,所以梁图像有且只有一个交点,即原函数有且只有一个零点。故C正确。
,所以梁图像有且只有一个交点,即原函数有且只有一个零点。故C正确。
考点:函数的零点

练习册系列答案
相关题目
设 ,则
,则 的大小关系是( )
的大小关系是( )
A. | B. | C. | D. |
设f(x)=(1+ )x-
)x- . 其中
. 其中 ,t为常数;集合M={x
,t为常数;集合M={x ﹤0,
﹤0, },则对任意实常数t,总有
},则对任意实常数t,总有
A.-3 M,0 M,0 M M | B.-3 M,0 M,0 M M |
C.-3 M,0 M,0 M M | D.-3 M,0 M,0 M M |
函数f(x)=x3-2x2+3x-6在区间[-2,4]上的零点必在所在区间是 ( )
| A.[-2,1] | B.[ ,4] ,4] | C.[1, ] ] | D.[ , , ] ] |
已知函数 则
则 ( )
( )
A. | B. | C. | D. |
若函数 则
则 (e为自然对数的底数)=( )
(e为自然对数的底数)=( )
| A.0 | B.1 | C.2 | D. |
已知 ,且
,且 ,
, ,则
,则 等于
等于
A. | B. | C. | D. |
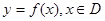 ,若存在常数
,若存在常数 ,对任意
,对任意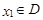 ,存在唯一
,存在唯一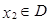 的,使得
的,使得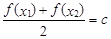 ,则称函数
,则称函数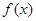 在
在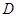 上的均值为
上的均值为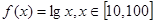 ,则函数
,则函数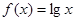 在
在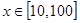 上的均值为( )
上的均值为( )
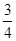
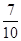
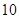
 和
和 ,定义运算“*”:
,定义运算“*”:  设
设 ,且关于
,且关于 的方程为
的方程为 恰有三个互不相等的实数根
恰有三个互不相等的实数根 、
、 、
、 ,则
,则 的取值范围是( )
的取值范围是( )


