题目内容
若∠ACB=90°在平面α内,PC与CA、CB所成的角∠PCA=∠PCB=60°,则PC与平面α所成的角为 45°.
【答案】分析:PC与平面α所成的角实际上是pc与pc在α上的射影所成的角,作PO⊥α于点O,则CO平分∠ACB,∠BCO=45°,
作OD⊥BC于点D,则PD⊥BC,∠PCO为pc与平面α所成的角的平面角;或者由三余弦定理解决.
解答:解:作PO⊥α于点O,则CO平分∠ACB,∠BCO=45°,
作OD⊥BC于点D,则PD⊥BC.
于是CD=PCcos60°= PC,CO=
PC,CO= =
= PC,∴cos∠PCO=
PC,∴cos∠PCO= =
= ,
,
即∠PCO=45°.
或由cos60°=cosθ•cos45°θ=45°(θ为PC与平面α所成的角).
故答案为:45°
点评:此题是直线与平面所成的角的题,需要学生有较强的转换思想
作OD⊥BC于点D,则PD⊥BC,∠PCO为pc与平面α所成的角的平面角;或者由三余弦定理解决.
解答:解:作PO⊥α于点O,则CO平分∠ACB,∠BCO=45°,
作OD⊥BC于点D,则PD⊥BC.
于是CD=PCcos60°=
 PC,CO=
PC,CO= =
= PC,∴cos∠PCO=
PC,∴cos∠PCO= =
= ,
,即∠PCO=45°.
或由cos60°=cosθ•cos45°θ=45°(θ为PC与平面α所成的角).
故答案为:45°
点评:此题是直线与平面所成的角的题,需要学生有较强的转换思想

练习册系列答案
相关题目
平面上有三个点
A、B、C,坐标分别是(1,3),(7,y),(2,2),若∠ACB=90°,则y值为[
]|
A .9 |
B .8 |
C .7 |
D .6 |
 (2011•孝感模拟)如图,已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,侧棱与底面所成的角为θ,且
(2011•孝感模拟)如图,已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,侧棱与底面所成的角为θ,且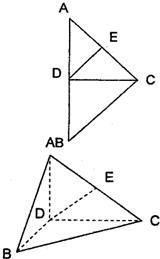 如图,在Rt△ABC中,∠ACB=90°,AC=BC=4,D是AB中点,E是AC的中点,现将△ABC沿CD翻折成直二面角A-DC-B.
如图,在Rt△ABC中,∠ACB=90°,AC=BC=4,D是AB中点,E是AC的中点,现将△ABC沿CD翻折成直二面角A-DC-B.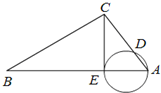 (几何证明选讲选做题)如图3,在△ABC中,∠ACB=90°,CE⊥AB于点E,以AE为直径的圆与AC交于点D,若BE=2AE=4,CD=3,则AC=
(几何证明选讲选做题)如图3,在△ABC中,∠ACB=90°,CE⊥AB于点E,以AE为直径的圆与AC交于点D,若BE=2AE=4,CD=3,则AC=