题目内容
(本题12分)直线l:y=kx+1与双曲线C: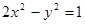 的右支交于不同的两点A,B.
的右支交于不同的两点A,B.
(Ⅰ)求实数k的取值范围;
(Ⅱ)是否存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F?若存在,求出k的值;若不存在,说明理由.
【答案】
(Ⅰ)-2<k<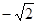 ;
;
(Ⅱ)k=- 时,使得以线段AB为直径的圆经过双曲线C的右焦点.
时,使得以线段AB为直径的圆经过双曲线C的右焦点.
【解析】
试题分析:(Ⅰ)由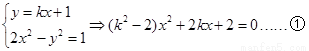
据题意: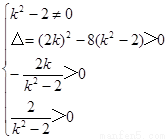 解得-2<k<
解得-2<k<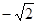 ……………5分
……………5分
(Ⅱ)设A,B两点的坐标分别为(x1,y1),(x2,y2), 则由①式得:
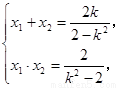
假设存在实数k,使得以线段AB为直径的圆过双曲线C的右焦点F(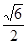 ,0),则FA
,0),则FA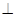 FB.
FB.
即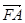 ·
·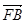 =0,(x1-
=0,(x1-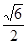 )(x2-
)(x2-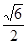 )+y1y2=0,
)+y1y2=0,
(x1-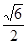 )(x2-
)(x2-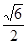 )+(kx1+1)(kx2+1)=0,
)+(kx1+1)(kx2+1)=0,
(1+k2)x1
x2+(k-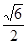 )(x1+ x2)+
)(x1+ x2)+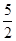 =0,
=0,
∴(1+k2)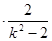 +(k-
+(k-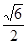 )·
)·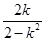 +
+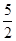 =0,
=0,
∴5k2+2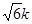 -6=0
-6=0
∴k=- 或k=
或k= ,
,
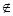 (-2,-
(-2,-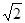 )(舍去)
)(舍去)
∴k=- 时,使得以线段AB为直径的圆经过双曲线C的右焦点.…………………12分
时,使得以线段AB为直径的圆经过双曲线C的右焦点.…………………12分
考点:本题主要考查直线与双曲线的位置关系。
点评:中档题,涉及直线与圆锥曲线的位置关系问题,往往要利用韦达定理。存在性问题,往往从假设存在出发,运用题中条件探寻得到存在的是否条件具备。

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目

 的等腰梯形ABCD,底边BC长为7cm,腰长为
的等腰梯形ABCD,底边BC长为7cm,腰长为 cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=
cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF= ,试写出左边部分的面积
,试写出左边部分的面积 与
与
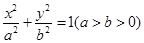 的两个焦点为F1,F2,点P在椭圆C上,且
的两个焦点为F1,F2,点P在椭圆C上,且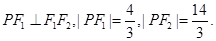 (1)求椭圆C的方程;
(1)求椭圆C的方程;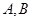 两点,且A、B关于点M对称,求直线l的方程.
两点,且A、B关于点M对称,求直线l的方程.