Question

如图，在直三棱柱ABC-A₁B₁C₁中，∠ACB=90°，AC=BC=CC₁=2．
（1）求证：AB₁⊥BC₁．
（2）求：二面角C-AC₁-B的大小．

Answer 1

分析：（1）根据直三棱柱的几何特征，侧面与底面垂直，结合∠ACB=90°，由面面垂直的性质定理易得AC⊥平面BCC₁B₁，又由AC=BC=CC₁=2，可得BCC₁B₁为正方形，即BC₁⊥B₁C，进而由三垂线定理得到AB₁⊥BC₁．
（2）连接A₁C交AC₁于点O，连接BO，由线面垂直的判定定理可证明BC⊥平面ACC₁，进而BO⊥AC₁，结合二面角的定义可得∠BOC即为二面角C-AC₁-B的平面角，解Rt△BCO可得答案．

解答：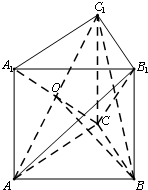
证明：（1）∵直三棱柱ABC-A₁B₁C₁中，AC⊥BC，
∴AC⊥平面BCC₁B₁，
连接B₁C，则∵BCC₁B₁为正方形，
∴BC₁⊥B₁C，
∴由三垂线定理知：AB₁⊥BC₁．…（6分）
解：（2）连接A₁C交AC₁于点O，连接BO，
则：∵BC⊥AC，BC⊥CC₁，
∴BC⊥平面ACC₁，又CO⊥AC₁，
∴BO⊥AC₁，
∴∠BOC即为二面角C-AC₁-B的平面角…（10分）
在Rt△BCO中：BC=2，  CO=

2

，
∴tan∠BOC=

BC

CO

=

2

∴二面角C-AC₁-B的大小为：arctan

2

．…（13分）

点评：本题考查的知识点是二面角的求法，空间中直线与直线之间的位置关系，其中解答（1）的关键是熟练掌握空间线线垂直与线面垂直之间的相互转化，（2）的关键是构造出二面角C-AC₁-B的平面角∠BOC．