题目内容
已知函数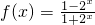 .
.
(1)试确定f(x)的奇偶性;
(2)求证:函数f(x)在R上是减函数;
(3)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
解:(1)由于函数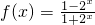 的定义域为R,关于原点对称,且有f(-x)=
的定义域为R,关于原点对称,且有f(-x)= =
= =-
=- =-f(x),故函数f(x)为奇函数.
=-f(x),故函数f(x)为奇函数.
(2)∵f(x)=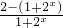 =
= -1,设x1<x2,再由f(x1)-f(x2)=(
-1,设x1<x2,再由f(x1)-f(x2)=(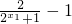 )-(
)-(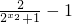 )=
)=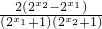 >0,
>0,
可得f(x1)>f(x2),故函数f(x)在R上是减函数.
(3)∵对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,f(x)为奇函数,∴f(t2-2t)<-f(2t2-k)=f(k-2t2) 恒成立.
再由函数f(x)在R上是减函数可得 t2-2t>k-2t2 恒成立,即 3 t2-2t-k>0恒成立.
∴△=4+12k<0,解得k<- ,
,
故k的取值范围为(-∞,- ).
).
分析:(1)由于函数的定义域为R,关于原点对称,且花简求得f(-x)=-f(x),由此可得函数f(x)为奇函数.
(2)化简函数f(x) 的解析式为 -1,设x1<x2,化简f(x1)-f(x2)=
-1,设x1<x2,化简f(x1)-f(x2)=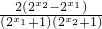 >0,可得函数f(x)在R上是减函数.
>0,可得函数f(x)在R上是减函数.
(3)由于f(x)为奇函数,不等式即 f(t2-2t)<f(k-2t2) 恒成立.再由函数f(x)在R上是减函数可得 t2-2t>k-2t2 恒成立,即 3 t2-2t-k>0恒成立.
由判别式△<0,解得k的取值范围.
点评:本题主要考查指数型复合函数的性质以及应用,二次函数的性质,函数的恒成立问题,属于中档题.
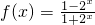 的定义域为R,关于原点对称,且有f(-x)=
的定义域为R,关于原点对称,且有f(-x)= =
= =-
=- =-f(x),故函数f(x)为奇函数.
=-f(x),故函数f(x)为奇函数.(2)∵f(x)=
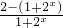 =
= -1,设x1<x2,再由f(x1)-f(x2)=(
-1,设x1<x2,再由f(x1)-f(x2)=(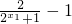 )-(
)-(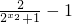 )=
)=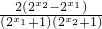 >0,
>0,可得f(x1)>f(x2),故函数f(x)在R上是减函数.
(3)∵对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,f(x)为奇函数,∴f(t2-2t)<-f(2t2-k)=f(k-2t2) 恒成立.
再由函数f(x)在R上是减函数可得 t2-2t>k-2t2 恒成立,即 3 t2-2t-k>0恒成立.
∴△=4+12k<0,解得k<-
 ,
,故k的取值范围为(-∞,-
 ).
).分析:(1)由于函数的定义域为R,关于原点对称,且花简求得f(-x)=-f(x),由此可得函数f(x)为奇函数.
(2)化简函数f(x) 的解析式为
 -1,设x1<x2,化简f(x1)-f(x2)=
-1,设x1<x2,化简f(x1)-f(x2)=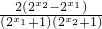 >0,可得函数f(x)在R上是减函数.
>0,可得函数f(x)在R上是减函数.(3)由于f(x)为奇函数,不等式即 f(t2-2t)<f(k-2t2) 恒成立.再由函数f(x)在R上是减函数可得 t2-2t>k-2t2 恒成立,即 3 t2-2t-k>0恒成立.
由判别式△<0,解得k的取值范围.
点评:本题主要考查指数型复合函数的性质以及应用,二次函数的性质,函数的恒成立问题,属于中档题.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
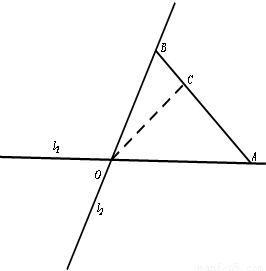
 (2012•江苏二模)如图,在C城周边已有两条公路l1,l2在点O处交汇,现规划在公路l1,l2上分别选择A,B两处为交汇点(异于点O)直接修建一条公路通过C城,已知OC=
(2012•江苏二模)如图,在C城周边已有两条公路l1,l2在点O处交汇,现规划在公路l1,l2上分别选择A,B两处为交汇点(异于点O)直接修建一条公路通过C城,已知OC=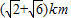 ,∠AOB=75°,∠AOC=45°,设OA=xkm,OB=ykm.
,∠AOB=75°,∠AOC=45°,设OA=xkm,OB=ykm.
 ,∠AOB=75°,∠AOC=45°,设OA=xkm,OB=ykm.
,∠AOB=75°,∠AOC=45°,设OA=xkm,OB=ykm.