题目内容
过原点O作圆x2+y2-6x-8y+20=0的两条切线，设切点分别为P、Q，则线段PQ的长为分析：如图：先求出圆心坐标和半径，直角三角形中使用边角关系求出cosα，二倍角公式求出cos∠PO1Q，三角形PO1Q中，
用余弦定理求出|PQ|．
用余弦定理求出|PQ|．
解答：
解：圆x2+y2-6x-8y+20=0 可化为 （x-3）2+（y-4）2 =5，
圆心（3，4）到原点的距离为5．故cosα=
，
∴cos∠PO1Q=2cos2α-1=-
，
∴|PQ|2=（
）2+（
）2+2×（
）2×
=16．∴|PQ|=4．
故答案为：4．
解：圆x2+y2-6x-8y+20=0 可化为 （x-3）2+（y-4）2 =5，圆心（3，4）到原点的距离为5．故cosα=
| ||
| 5 |
∴cos∠PO1Q=2cos2α-1=-
| 3 |
| 5 |
∴|PQ|2=（
| 5 |
| 5 |
| 5 |
| 3 |
| 5 |
故答案为：4．
点评：本题考查直角三角形中的边角关系，二倍角的余弦公式，以及用余弦定理求边长．
练习册系列答案
仁爱英语同步练习册系列答案
学习实践园地系列答案
相关题目
过原点O作圆x2+y2-8x=0的弦OA．
（1）求弦OA中点M的轨迹方程；
（2）如果M（x，y）是（1）中的轨迹上的动点，
①求T=x2+y2+4x-6y的最大、最小值；
②求N=
的最大、最小值．
（1）求弦OA中点M的轨迹方程；
（2）如果M（x，y）是（1）中的轨迹上的动点，
①求T=x2+y2+4x-6y的最大、最小值；
②求N=
| y | x+2 |
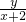的最大、最小值．
的最大、最小值．
的最大、最小值．