题目内容
函数f(x)的定义域为R,并满足以下条件:
①对任意的x∈R,有f(x)>0;
②对任意的x,y∈R,都有f(xy)=[f(x)]y;
③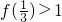 .
.
(Ⅰ)求f(0)的值;
(Ⅱ)求证:f(x)是(-∞,+∞)上的单调递增函数;
(Ⅲ)解关于x的不等式:[f(x-2a)](x+1)>1.
解:(1):(1)∵对任意x∈R,有f(x)>0,
∴令x=0,y=2得:f(0)=[f(0)]2?f(0)=1;
(2)任取x1,x2∈R,且x1<x2,则令x1= P1,x2=
P1,x2= P2,故p1<p2,
P2,故p1<p2,
∵函数f(x)的定义域为R,并满足以下条件:①对任意x∈R,有f(x)>0;②对任意x,y∈R,有f(xy)=[f(x)]y;③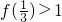
∴f(x1)-f(x2)=f( P1)-f(
P1)-f( P2)=[f(
P2)=[f( )]P1-[f(
)]P1-[f( )]P2<0,
)]P2<0,
∴f(x1)<f(x2),
∴函数f(x)是R上的单调增函数.
(3)∵解关于x的不等式:[f(x-2a)](x+1)>1=f(0),f(x)是(-∞,+∞)上的单调递增函数,
∴f(x-2a)x+1>0,
∴f[(x-2a)(x+1)]=f(x-2a)x+1>0,∵对任意的x∈R,有f(x)>0;
∴(x-2a)(x+1)>0,比较2a与-1的大小
当 时,f(x)的解集为(-∞,-1)∪(-1,+∞);
时,f(x)的解集为(-∞,-1)∪(-1,+∞);
当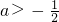 时,即2a>-1,f(x)的解集为(-∞,-1)∪(2a,+∞);
时,即2a>-1,f(x)的解集为(-∞,-1)∪(2a,+∞);
当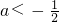 时,即2a<-1,f(x)的解集为(-∞,2a)∪(-1,+∞).
时,即2a<-1,f(x)的解集为(-∞,2a)∪(-1,+∞).
分析:(Ⅰ)可以令y=0,代入f(xy)=[f(x)]y,即可求得f(0)的值;
(Ⅱ)任取x1,x2∈R,且x1<x2,可令x1= P1,x2=
P1,x2= P2,故p1<p2,再判断f(x1)-f(x2)的符号,从而可证其单调性;,
P2,故p1<p2,再判断f(x1)-f(x2)的符号,从而可证其单调性;,
(Ⅲ)根据f(x)是增函数,利用f(0)=1,代入不等式,再利用单调性进行求解;
点评:本题考查抽象函数及其应用,难点在于用单调函数的定义证明其单调递增时“任取x1,x2∈R,且x1<x2,则x1= P1,x2=
P1,x2= P2,”这一步比较灵活需要学生的理解与应用,属于中档题.
P2,”这一步比较灵活需要学生的理解与应用,属于中档题.
∴令x=0,y=2得:f(0)=[f(0)]2?f(0)=1;
(2)任取x1,x2∈R,且x1<x2,则令x1=
 P1,x2=
P1,x2= P2,故p1<p2,
P2,故p1<p2,∵函数f(x)的定义域为R,并满足以下条件:①对任意x∈R,有f(x)>0;②对任意x,y∈R,有f(xy)=[f(x)]y;③
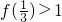
∴f(x1)-f(x2)=f(
 P1)-f(
P1)-f( P2)=[f(
P2)=[f( )]P1-[f(
)]P1-[f( )]P2<0,
)]P2<0,∴f(x1)<f(x2),
∴函数f(x)是R上的单调增函数.
(3)∵解关于x的不等式:[f(x-2a)](x+1)>1=f(0),f(x)是(-∞,+∞)上的单调递增函数,
∴f(x-2a)x+1>0,
∴f[(x-2a)(x+1)]=f(x-2a)x+1>0,∵对任意的x∈R,有f(x)>0;
∴(x-2a)(x+1)>0,比较2a与-1的大小
当
 时,f(x)的解集为(-∞,-1)∪(-1,+∞);
时,f(x)的解集为(-∞,-1)∪(-1,+∞);当
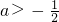 时,即2a>-1,f(x)的解集为(-∞,-1)∪(2a,+∞);
时,即2a>-1,f(x)的解集为(-∞,-1)∪(2a,+∞);当
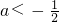 时,即2a<-1,f(x)的解集为(-∞,2a)∪(-1,+∞).
时,即2a<-1,f(x)的解集为(-∞,2a)∪(-1,+∞).分析:(Ⅰ)可以令y=0,代入f(xy)=[f(x)]y,即可求得f(0)的值;
(Ⅱ)任取x1,x2∈R,且x1<x2,可令x1=
 P1,x2=
P1,x2= P2,故p1<p2,再判断f(x1)-f(x2)的符号,从而可证其单调性;,
P2,故p1<p2,再判断f(x1)-f(x2)的符号,从而可证其单调性;,(Ⅲ)根据f(x)是增函数,利用f(0)=1,代入不等式,再利用单调性进行求解;
点评:本题考查抽象函数及其应用,难点在于用单调函数的定义证明其单调递增时“任取x1,x2∈R,且x1<x2,则x1=
 P1,x2=
P1,x2= P2,”这一步比较灵活需要学生的理解与应用,属于中档题.
P2,”这一步比较灵活需要学生的理解与应用,属于中档题. 
练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
若函数f(x)的定义域为[-1,2],则函数
的定义域为( )
| f(x+2) |
| x |
| A、[-1,0)∪(0,2] |
| B、[-3,0) |
| C、[1,4] |
| D、(0,2] |