题目内容
如图1-3-17,点C、D在线段AB上,△PCD是等边三角形.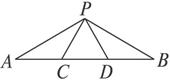
图1-3-17
(1)当AC、CD、DB满足怎样的关系时,△ACP∽△PDB?
(2)当△ACP∽△PDB时,求∠APB的度数.
思路分析:本题是一个探索型的问题,考查相似三角形的判定及性质,它给出了一个条件,让你自己再添加一个条件,可使两个三角形相似.因此,首先想到相似的判定方法,因又限制了三条边的关系,所以是对应边就成比例.当三角形相似以后,那么对应角相等,易求∠APB.
解:(1)∵△PCD是等边三角形,
∴∠PCD=∠PDC=60°,PD=PC=CD.
从而∠ACP=∠PDB=120°.
∴当![]() 时,△ACP∽△PDB.
时,△ACP∽△PDB.
即当CD2=AC·BD时,△ACP∽△PDB.
(2)当△ACP∽△PDB时,∠APC=∠PBD.
∴∠APB=∠APC+∠CPD+∠DPB
=∠PBD+60°+∠DPB
=60°+60°=120°.

练习册系列答案
相关题目