题目内容
(选做题)设a，b，c均为正实数．
（1）若a+b+c=1，求a2+b2+c2的最小值；
（2）求证：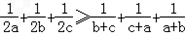
．
（1）若a+b+c=1，求a2+b2+c2的最小值；
（2）求证：
．
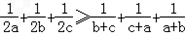解:（1）因为a，b，c 均为正实数，由柯西不等式得，
（a2+b2+c2）（12+12+12）≥（a+b+c）2=1，当且仅当a=b=c=
时等号成立，
∴a2+b2+c2 的最小值为
．
（2）∵a，b，c均为正实数，
∴可得
（ 
+
）≥ 
≥ 
，
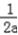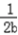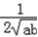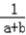同理
（ 
+
）≥ 
， 
（ 
+ 
）≥ 
，
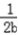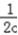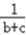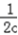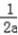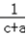三个不等式相加得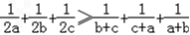
，
当且仅当a=b=c时等号成立．
（a2+b2+c2）（12+12+12）≥（a+b+c）2=1，当且仅当a=b=c=
时等号成立，∴a2+b2+c2 的最小值为
． （2）∵a，b，c均为正实数，
∴可得
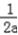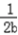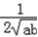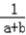（ + ）≥ ≥ ，同理
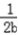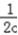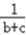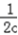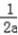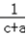（ + ）≥ ， （ + ）≥ ，三个不等式相加得
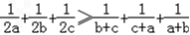，当且仅当a=b=c时等号成立．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
期末集结号系列答案
相关题目
选做题（在A、B、C、D四小题中只能选做两题，并将选作标记用2B铅笔涂黑，每小题10分，共20分，请在答题指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）．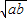
（a+b）．