题目内容
(1)已知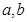 是正常数,
是正常数, ,
,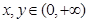 ,求证:
,求证: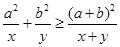 ,指出等号成立的条件;
,指出等号成立的条件;
(2)利用(1)的结论求函数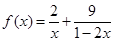 (
( )的最小值,指出取最小值时
)的最小值,指出取最小值时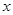 的值.
的值.
【答案】
(1) 见解析(2)  时上式取最小值,即
时上式取最小值,即
【解析】本试题主要是考查了均值不等式和函数的最值的运用。给你一种解题工具,让你应用它来解答某一问题,这是近年考试命题的一种新颖的题型之一,很值得考生深刻反思和领悟当中的思维本质。
(1)应用均值不等式,得

 ,变形得到。
,变形得到。
(2)由(1) ,那么可知当
,那么可知当 上式得到最小值。
上式得到最小值。
解:(1)应用均值不等式,得

 ,
,
故 .…………………5分
.…………………5分
当且仅当 ,即
,即 时上式取等号.……………6分
时上式取等号.……………6分
(用比较法证明的自己给标准给分)
(2)由(1) .
.
当且仅当 ,即
,即 时上式取最小值,即
时上式取最小值,即 .……12分
.……12分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
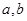 是正常数,
是正常数, ,
, ,求证:
,求证: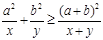 ,指出等号成立的条件;
,指出等号成立的条件;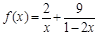 (
( )的最小值,并指出取最小值时
)的最小值,并指出取最小值时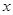 的值.
的值.