题目内容
(2013•汕头二模)已知向量
=(
),
=(cosx,sinx);
(1)若
⊥
,求tan(x-
)的值;
(2)若函数f(x)=
•
,求函数f(x)的最小正周期和单调递增区间.
| a |
| 1 |
| 2, |
| ||
| 2 |
| b |
(1)若
| a |
| b |
| π |
| 4 |
(2)若函数f(x)=
| a |
| b |
分析:(1)通过数量积求出x的正切值,利用两角差的正切函数展开表达式,求解即可.
(2)求出函数的表达式,利用两角和与差的三角函数,化简表达式,通过三角函数的周期公式求出周期,利用正弦函数的单调性求出单调增区间即可.
(2)求出函数的表达式,利用两角和与差的三角函数,化简表达式,通过三角函数的周期公式求出周期,利用正弦函数的单调性求出单调增区间即可.
解答:解:因为向量
=(
,
),
=(cosx,sinx);
⊥
,
所以
•
=0即
cosx+
sinx=0∴tanx=-
.
tan(x-
)=
=
=-2-
.
(2)因为函数f(x)=
•
=
cosx+
sinx=sin(x+
)所以函数的周期是T=
=2π,
令-
+2kπ≤x+
≤
+2kπ k∈Z,
解得:-
+2kπ≤x≤
+2kπ k∈Z,
所以函数的单调增区间为:[-
+2kπ,
+2kπ] k∈Z.
| a |
| 1 |
| 2 |
| ||
| 2 |
| b |
| a |
| b |
所以
| a |
| b |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 3 |
tan(x-
| π |
| 4 |
| tanx-1 |
| tanx+1 |
-
| ||||
1-
|
| 3 |
(2)因为函数f(x)=
| a |
| b |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 6 |
| 2π |
| 1 |
令-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
解得:-
| 2π |
| 3 |
| π |
| 3 |
所以函数的单调增区间为:[-
| 2π |
| 3 |
| π |
| 3 |
点评:本题考查数量积的应用,三角函数的化简求值,两角和与差的三角函数以及三角函数的单调性的应用,考查计算能力.

练习册系列答案
相关题目
 (2013•汕头二模)执行框图,若输出结果为
(2013•汕头二模)执行框图,若输出结果为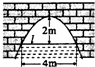 (2013•汕头二模)如图是抛物线形拱桥,当水面在l时,拱顶离水面2米,水面宽4米,水位下降2米后水面宽
(2013•汕头二模)如图是抛物线形拱桥,当水面在l时,拱顶离水面2米,水面宽4米,水位下降2米后水面宽