题目内容
设O为坐标原点，点A（4，3），B是x正半轴上一点，则△OAB中
的最大值为（ ）
| OB |
| AB |
分析：根据三角函数的定义，算出sin∠AOB=
．结合正弦定理得到
=
=
sinA，再根据sinA≤1，即可得到当且仅当A=
时，
的最大值为
．
| 3 |
| 5 |
| OB |
| AB |
| sinA |
| sin∠AOB |
| 5 |
| 3 |
| π |
| 2 |
| OB |
| AB |
| 5 |
| 3 |
解答：解：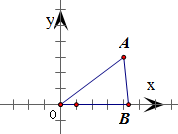
∵A（4，3），
∴根据三角函数的定义，得sin∠AOB=
．
由正弦定理，得
=
∴
=
=
sinA
由A∈（0，π），得sinA∈（0，1]
∴当A=
时，
=
sinA的最大值为
故选：B
∵A（4，3），∴根据三角函数的定义，得sin∠AOB=
| 3 |
| 5 |
由正弦定理，得
| AB |
| sin∠AOB |
| OB |
| sinA |
∴
| OB |
| AB |
| sinA |
| sin∠AOB |
| 5 |
| 3 |
由A∈（0，π），得sinA∈（0，1]
∴当A=
| π |
| 2 |
| OB |
| AB |
| 5 |
| 3 |
| 5 |
| 3 |
故选：B
点评：本题在坐标系中，已知A（4，3）且B是x正半轴上一点，求
的最大值．着重考查了三角函数的定义和正弦定理等知识，属于基础题．
| OB |
| AB |
练习册系列答案
阅读快车系列答案
相关题目