题目内容
已知向量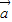 =(cosα,sinα),
=(cosα,sinα),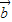 =(cosβ,sinβ),|
=(cosβ,sinβ),|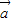 -
-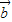 |=
|=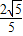 .
.(1)求cos(α-β)的值;
(2)若0<α<
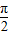 ,-
,-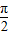 <β<0,且sinβ=-
<β<0,且sinβ=-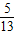 ,求sinα的值.
,求sinα的值.
【答案】分析:(1)通过|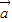 -
-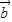 |=
|=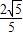 .求出向量的模,化简即可求出cos(α-β)的值;
.求出向量的模,化简即可求出cos(α-β)的值;
(2)通过0<α<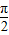 ,-
,-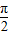 <β<0,且sinβ=-
<β<0,且sinβ=-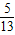 ,求出cosβ的值,sin(α-β)的值,利用sinα=sin(α-β+β),然后求sinα的值.
,求出cosβ的值,sin(α-β)的值,利用sinα=sin(α-β+β),然后求sinα的值.
解答:解:(1)因为向量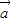 =(cosα,sinα),
=(cosα,sinα),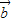 =(cosβ,sinβ),|
=(cosβ,sinβ),|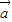 -
-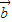 |=
|=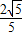 =
=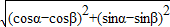 =
=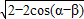 ,所以2-2cos(α-β)=
,所以2-2cos(α-β)= ,
,
所以cos(α-β)= ;
;
(2)若0<α<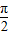 ,-
,-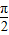 <β<0,所以0<α-β<π,因为cos(α-β)=
<β<0,所以0<α-β<π,因为cos(α-β)= ,所以sin(α-β)=
,所以sin(α-β)=
且sinβ=-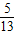 ,cosβ=
,cosβ=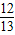 ,
,
所以,sinα=sin(α-β+β)=sin(α-β)cosβ+cos(α-β)sinβ=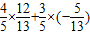 =
=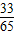
点评:本题是中档题,考查三角函数的恒等变换以及化简求值,平面向量的数量积的应用,注意角的变换的技巧α=α-β+β,是简化解题过程的依据,注意角的范围的确定,是解题的关键,同时注意:3,4,5;5,12,13.这些特殊数字组成的直角三角形的三角函数值的应用.
 -
-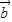 |=
|=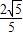 .求出向量的模,化简即可求出cos(α-β)的值;
.求出向量的模,化简即可求出cos(α-β)的值;(2)通过0<α<
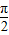 ,-
,-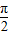 <β<0,且sinβ=-
<β<0,且sinβ=-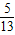 ,求出cosβ的值,sin(α-β)的值,利用sinα=sin(α-β+β),然后求sinα的值.
,求出cosβ的值,sin(α-β)的值,利用sinα=sin(α-β+β),然后求sinα的值.解答:解:(1)因为向量
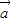 =(cosα,sinα),
=(cosα,sinα),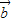 =(cosβ,sinβ),|
=(cosβ,sinβ),|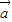 -
-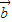 |=
|=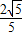 =
=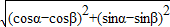 =
=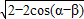 ,所以2-2cos(α-β)=
,所以2-2cos(α-β)= ,
,所以cos(α-β)=
 ;
;(2)若0<α<
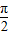 ,-
,-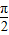 <β<0,所以0<α-β<π,因为cos(α-β)=
<β<0,所以0<α-β<π,因为cos(α-β)= ,所以sin(α-β)=
,所以sin(α-β)=
且sinβ=-
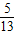 ,cosβ=
,cosβ=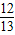 ,
,所以,sinα=sin(α-β+β)=sin(α-β)cosβ+cos(α-β)sinβ=
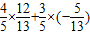 =
=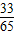
点评:本题是中档题,考查三角函数的恒等变换以及化简求值,平面向量的数量积的应用,注意角的变换的技巧α=α-β+β,是简化解题过程的依据,注意角的范围的确定,是解题的关键,同时注意:3,4,5;5,12,13.这些特殊数字组成的直角三角形的三角函数值的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知向量
=(cosα,sinα),
=(cosβ,sinβ),若|
-
|=
,则
和
的夹角为( )
| a |
| b |
| a |
| b |
| 2 |
| a |
| b |
| A、60° | B、90° |
| C、120° | D、150° |