题目内容
在曲线y=x2+1的图像上取一点(1,2),及邻近一点(1+Δx,2+Δy),则A.Δx+![]() B.Δx
B.Δx![]() -2 C.Δx+2 D.2+Δx
-2 C.Δx+2 D.2+Δx![]()
答案:C Δy=f(1+Δx)-f(1)=(1+Δx)2+1-(12+1)=(Δx)2+2Δx,![]() =Δx+2.
=Δx+2.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
在曲线y=x2+1的图象上取一点(1,2)及邻近一点(1+△x,2+△y),则△y:△x为( )
A、△x+
| ||
B、△x-
| ||
| C、△x+2 | ||
D、2+△x-
|
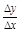 为 .
为 .