题目内容
已知直线x+y=a与圆x2+y2=4交于A、B两点,且|A.2 B.-2 C.2或-2 D.![]() 或-
或-![]()
解析:由|![]() +
+![]() |=|
|=|![]() -
-![]() |,知
|,知![]() ⊥
⊥![]() ,
,
由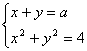 消去y得x2+(a-x)2=4,即2x2-2ax+a2-4=0.
消去y得x2+(a-x)2=4,即2x2-2ax+a2-4=0.
设A(x1,y1),B(x2,y2),则x1+x2=a,x1·x2=![]() .
.
∵OA⊥OB,∴![]() ·
·![]() =0.
=0.
∴x1x2+y1y2=0,即x1x2+(a-x1)·(a-x2)=0.
∴2x1x2-a(x1+x2)+a2=0,∴a2-4-a2+a2=0∴a=±2.
答案:C

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知直线x+y=a与圆x2+y2=4交于A、B两不同点,O是坐标原点,向量
、
满足
•
=0,则实数a的值是( )
| OA |
| OB |
| OA |
| OB |
| A、2 | ||
| B、±2 | ||
C、±
| ||
| D、-2 |
已知直线x+y=a与圆x2+y2=4交于A、B两点,O是坐标原点,向量
、
满足|
+
|=|
-
,则实数a的值( )
| OA |
| OB |
| OA |
| OB |
| OA |
| OB| |
| A、2 | ||||
| B、-2 | ||||
C、
| ||||
| D、2或-2 |