题目内容
已知M是y=
x2上一点，F为抛物线焦点，A在C：（x-1）2+（y-4）2=1上，则|MA|+|MF|的最小值
- A.2
- B.4
- C.8
- D.10
B
分析：将抛物线化成标准方程，求得其准线为l：y=-1，过点M作MN⊥l于N，由抛物线定义得|MN|=|MF|，问题转化为求|MA|+|MN|的最小值，而A在圆C上运动，因此可得到当N、M、C三点共线时，|MA|+|MN|有最小值，进而求得|MA|+|MF|的最小值．
解答：∵抛物线y=x2化成标准方程为x2=4y，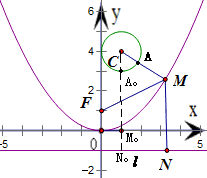
∴抛物线的准线为l：y=-1
过点M作MN⊥l于N，
∵|MN|=|MF|，∴|MA|+|MF|=|MA|+|MN|
∵A在圆C：（x-1）2+（y-4）2=1上运动，
圆心为C（1，4）且半径r=1
∴当N，M，C三点共线时，|MA|+|MF|最小
∴（|MA|+|MF|）min=（|MA|+|MN|）min=|CN0|-r=5-1=4
即|MA|+|MF|的最小值为4
故选：B
点评：本题给出抛物线张口以内的一个圆，求抛物线上动点M到圆上动点A的距离与A到焦点F距离之和的最小值，着重考查了求与圆有关的距离的最值、抛物线的定义与简单几何性质等知识，属于中档题．
分析：将抛物线化成标准方程，求得其准线为l：y=-1，过点M作MN⊥l于N，由抛物线定义得|MN|=|MF|，问题转化为求|MA|+|MN|的最小值，而A在圆C上运动，因此可得到当N、M、C三点共线时，|MA|+|MN|有最小值，进而求得|MA|+|MF|的最小值．
解答：∵抛物线y=
x2化成标准方程为x2=4y，∴抛物线的准线为l：y=-1
过点M作MN⊥l于N，
∵|MN|=|MF|，∴|MA|+|MF|=|MA|+|MN|
∵A在圆C：（x-1）2+（y-4）2=1上运动，
圆心为C（1，4）且半径r=1
∴当N，M，C三点共线时，|MA|+|MF|最小
∴（|MA|+|MF|）min=（|MA|+|MN|）min=|CN0|-r=5-1=4
即|MA|+|MF|的最小值为4
故选：B
点评：本题给出抛物线张口以内的一个圆，求抛物线上动点M到圆上动点A的距离与A到焦点F距离之和的最小值，着重考查了求与圆有关的距离的最值、抛物线的定义与简单几何性质等知识，属于中档题．
练习册系列答案
开心练习课课练与单元检测系列答案
相关题目
已知z是实系数方程x2+2bx+c=0的虚根，记它在直角坐标平面上的对应点为Pz，
（1）若（b，c）在直线2x+y=0上，求证：Pz在圆C1：（x-1）2+y2=1上；
（2）给定圆C：（x-m）2+y2=r2（m、r∈R，r＞0），则存在唯一的线段s满足：①若Pz在圆C上，则（b，c）在线段s上；②若（b，c）是线段s上一点（非端点），则Pz在圆C上、写出线段s的表达式，并说明理由；
（3）由（2）知线段s与圆C之间确定了一种对应关系，通过这种对应关系的研究，填写表（表中s1是（1）中圆C1的对应线段）．
（1）若（b，c）在直线2x+y=0上，求证：Pz在圆C1：（x-1）2+y2=1上；
（2）给定圆C：（x-m）2+y2=r2（m、r∈R，r＞0），则存在唯一的线段s满足：①若Pz在圆C上，则（b，c）在线段s上；②若（b，c）是线段s上一点（非端点），则Pz在圆C上、写出线段s的表达式，并说明理由；
（3）由（2）知线段s与圆C之间确定了一种对应关系，通过这种对应关系的研究，填写表（表中s1是（1）中圆C1的对应线段）．
| 线段s与线段s1的关系 | m、r的取值或表达式 |
| s所在直线平行于s1所在直线 | |
| s所在直线平分线段s1 |