题目内容
已知数列{an}的首项a1=1,a2=3,前n项的和为Sn,且Sn+1、Sn、Sn﹣1(n≥2)分别是直线l上的点A、B、C的横坐标,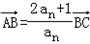 ,设b1=1,bn+1=log2(an+1)+bn.
,设b1=1,bn+1=log2(an+1)+bn.
(1)判断数列{an+1}是否为等比数列,并证明你的结论.
(2)设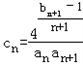 ,数列{cn}的前n项和为Tn,证明:Tn<1.
,数列{cn}的前n项和为Tn,证明:Tn<1.
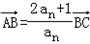 ,设b1=1,bn+1=log2(an+1)+bn.
,设b1=1,bn+1=log2(an+1)+bn.(1)判断数列{an+1}是否为等比数列,并证明你的结论.
(2)设
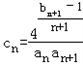 ,数列{cn}的前n项和为Tn,证明:Tn<1.
,数列{cn}的前n项和为Tn,证明:Tn<1.(1)解:判断数列{an+1}为等比数列,证明如下:
由题意Sn+1、Sn、Sn﹣1(n≥2)分别是直线l上的点A、B、C的横坐标,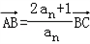 , 得
, 得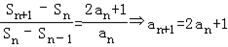
∴an+1+1=2(an+1)(n≥2),
又∵a1=1,a2=3
∴数列{an+1}是以a1+1=2为首项,以2为公比的等比数列.
则an+1=2n
∴an=2n﹣1(n∈N*)
(2)证明:由an=2n﹣1及bn+1=log2(an+1)+bn得bn+1=bn+n,
∴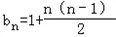 ,
,
则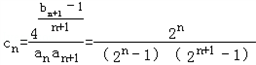 =
=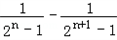 ,
,
数列{cn}的前n项和为Tn为:
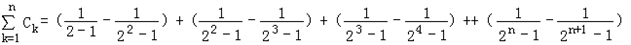 =
=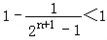 .
.
由题意Sn+1、Sn、Sn﹣1(n≥2)分别是直线l上的点A、B、C的横坐标,
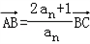 , 得
, 得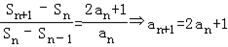
∴an+1+1=2(an+1)(n≥2),
又∵a1=1,a2=3
∴数列{an+1}是以a1+1=2为首项,以2为公比的等比数列.
则an+1=2n
∴an=2n﹣1(n∈N*)
(2)证明:由an=2n﹣1及bn+1=log2(an+1)+bn得bn+1=bn+n,
∴
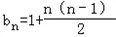 ,
, 则
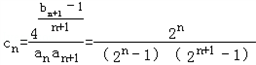 =
=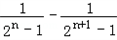 ,
,数列{cn}的前n项和为Tn为:
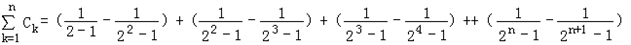 =
=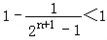 .
.
练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目