题目内容
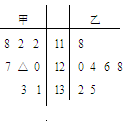
由于当前学生课业负担较重,造成青少年视力普遍下降,现从某高中随机抽取16名学生,经校医检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,
小数点后的一位数字为叶)如图示:
| | |
| 4 | 3 5 6 6 6 7 7 7 8 8 9 9 |
| 5 | 0 1 1 2 |
(2)若视力测试结果不低于5.0,则称为“健康视力”,求校医从这16人中随机选取3人,至多有1人是“健康视力”的概率;
(3)以这16人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记
 表示抽到“健康视力”学生的人数,求
表示抽到“健康视力”学生的人数,求 的分布列及数学期望
的分布列及数学期望
(1)众数为4.6和4.7;中位数为4.75(2) (3)
(3)
0 1 2 3 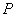





解析试题分析:(1)众数为4.6和4.7;中位数为4.75 ;
(2)设 表示所取3人中有
表示所取3人中有 (
( 的值为0,1)个人是“健康视力”,至多有1人是“健康视力”记为事件
的值为0,1)个人是“健康视力”,至多有1人是“健康视力”记为事件 ,则
,则
(3)由题意知, 的可能取值为0,1,2,3,
的可能取值为0,1,2,3, ,
,  ,
, ,
,
 的分布列为:
的分布列为:
0 1 2 3 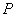





考点:古典概型概率与分布列期望
点评:众数是出现次数最多的数,中位数是将数据按大小排序后中间一个或两个的平均数;求分布列首先要确定随机变量可以取的值,然后依次求得各随机变量值的概率,即可求得分布列

 名校课堂系列答案
名校课堂系列答案2013年1月份,我国北方部分城市出现雾霾天气,形成雾霾天气主要原因与 有关.
有关.  是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.
是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.  日均值越小,空气质量越好. 2012年2月29日,国家环保部发布的《环境空气质量标准》见下表:
日均值越小,空气质量越好. 2012年2月29日,国家环保部发布的《环境空气质量标准》见下表:
 日均值k(微克) 日均值k(微克) | 空气质量等级 |
 | 一级 |
 | 二级 |
 | 超标 |

某环保部门为了了解甲、乙两市的空气质量状况,在过去某月的30天中分别随机抽取了甲、乙两市6天的
 日均值作为样本,样本数据茎叶图如上右图所示(十位为茎,个位为叶). (Ⅰ)分别求出甲、乙两市
日均值作为样本,样本数据茎叶图如上右图所示(十位为茎,个位为叶). (Ⅰ)分别求出甲、乙两市 日均值的样本平均数,并由此判断哪个市的空气质量较好;
日均值的样本平均数,并由此判断哪个市的空气质量较好;(Ⅱ)若从甲市这6天的样本数据中随机抽取两天的数据,求恰有一天空气质量超标的概率.
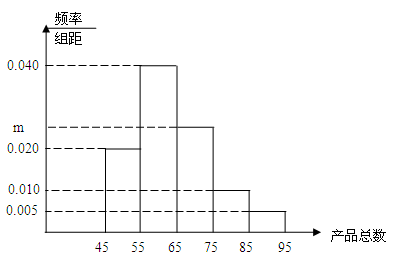
某种产品的广告费支出 与销售额
与销售额 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
 | 2 | 4 | 5 | 6 | 8 |
 | 30 | 40 | 60 | 50 | 70 |
(Ⅱ)试预测广告费支出为10万元时,销售额多大?
(Ⅲ)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率。
(参考数据:

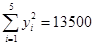
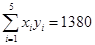 ,
,参考公式:回归直线方程
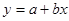 ,其中
,其中 )
) 在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)共有100个数据,将数据分组如表:
| 分组 | 频数 |
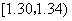 | 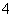 |
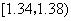 |  |
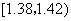 |  |
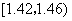 |  |
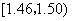 |  |
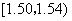 |  |
| 合计 |  |
(2)估计纤度落在
 中的概率及纤度小于
中的概率及纤度小于 的概率是多少?
的概率是多少?(3)从频率分布直方图估计出纤度的众数、中位数和平均数.
延迟退休年龄的问题,近期引发社会的关注.人社部于2012年7月25日上午召开新闻发布会表示,我国延迟退休年龄将借鉴国外经验,拟对不同群体采取差别措施,并以“小步慢走”的方式实施.推迟退休年龄似乎是一种必然趋势,然而反对的声音也随之而起.现对某市工薪阶层关于“延迟退休年龄”的态度进行调查,随机抽取了50人,他们月收入的频数分布及对“延迟退休年龄”反对的人数
| 月收入(元) | [1000,2000) | [2000,3000) | [3000,4000) | [4000,5000) | [5000,6000) | [6000,7000) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 反对人数 | 4 | 8 | 12 | 5 | 2 | 1 |
(2)若对月收入在[1000,2000),[4000,5000)的被调查对象中各随机选取两人进行跟踪调查,记选中的4人中赞成“延迟退休年龄”的人数为
 ,求
,求 的分布列和数学期望.
的分布列和数学期望. 为了解目前老年人居家养老还是在敬老院养老的意向,共调查了50名老年人,其中男性明确表示去敬老院养老的有5人,女性明确表示居家养老的有10人,已知在全部50人中随机地抽取1人明确表示居家养老的概率为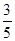 。
。
(1)请根据上述数据建立一个2×2列联表;(2)居家养老是否与性别有关?请说明理由。
参考数据:
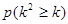 | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
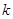 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
 的住户属于“低碳族”,则称这个小区为“低碳小区”,否则称为“非低碳小区”.已知备选的5个居民小区中有三个非低碳小区,两个低碳小区.
的住户属于“低碳族”,则称这个小区为“低碳小区”,否则称为“非低碳小区”.已知备选的5个居民小区中有三个非低碳小区,两个低碳小区.
 ,调查显示其“低碳族”的比例为
,调查显示其“低碳族”的比例为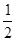 ,数据如图1所示,经过同学们的大力宣传,三个月后,又进行了一次调查,数据如图2所示,问这时小区
,数据如图1所示,经过同学们的大力宣传,三个月后,又进行了一次调查,数据如图2所示,问这时小区