题目内容
定义函数 (定义域),若存在常数C,对于任意
(定义域),若存在常数C,对于任意 ,存在唯一的
,存在唯一的 ,使得
,使得 ,则称函数
,则称函数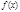 在D上的“均值”为C.已知
在D上的“均值”为C.已知 ,
, ,则函数
,则函数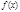 在
在 上的均值为( )
上的均值为( )
A. B.
B. C.
C. D.10
D.10
【答案】
C
【解析】
试题分析:根据定义,函数y=f(x),x∈D,若存在常数C,对任意的x1∈D,存在唯一的x2∈D,使得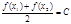 ,则称函数f(x)在D上的均值为C.
,则称函数f(x)在D上的均值为C.
令x1?x2=10×100=1000
当x1∈[10,100]时,选定x2=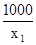 ∈[10,100],可得:C=
∈[10,100],可得:C=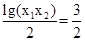 ,
,
故选C.
考点:新定义问题,对数函数的性质。
点评:中档题,理解题意是解题的关键,利用 ,构造符合题意的x1,x2。
,构造符合题意的x1,x2。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (定义域),若存在常数C,对于任意
(定义域),若存在常数C,对于任意 ,存在唯一的
,存在唯一的 ,使得
,使得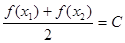 ,则称函数
,则称函数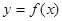 在D上的“均值”为C.已知函数
在D上的“均值”为C.已知函数 ,则函数
,则函数 上的均值为
( )
上的均值为
( ) (B)
(B) (C)10 (D)
(C)10 (D)
 (定义域),若存在常数C,对于任意
(定义域),若存在常数C,对于任意 ,存在唯一的
,存在唯一的 ,使得
,使得 ,则称函数
,则称函数 在D上的“均值”为C.已知函数
在D上的“均值”为C.已知函数 ,则函数
,则函数 上的均值为( )
上的均值为( ) (B)
(B) (C)10 (D)
(C)10 (D)
 (定义域),若存在常数C,对于任意
(定义域),若存在常数C,对于任意 ,存在唯一的
,存在唯一的 ,使得
,使得 ,则称函数
,则称函数 在D上的“均值”为C,已知
在D上的“均值”为C,已知 ,
, ,则函数
,则函数 上的均值为( )
上的均值为( ) B.
B. C.
C. D.10
D.10