题目内容
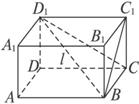
长方体ABCD—A1B1C1D1中:(1)设对角线D1B与自D1出发的三条棱分别成α、β、γ角,求证:cos2α+cos2β+cos2γ=1;
(2)设D1B与经过D1的三个表面成α、β、γ角,求证:cos2α+cos2β+cos2γ=2.
证明:(1)如图,连结BC1,不妨设∠BD1C1=α,长方体的三条棱长分别为a、b、c,设D1B=l,则cos2α=![]() .
.
同理,cos2β=![]() ,cos2γ=
,cos2γ=![]() .
.
∴cos2α+cos2β+cos2γ=![]() =1.
=1.
(2)连结D1C,
∵BC⊥平面DCC1D1,
∴∠BD1C就是D1B与平面DCC1D1所成的角,不妨设∠BD1C=α,则cos2α=![]() .
.
同理,cos2β=![]() ,cos2γ=
,cos2γ=![]() .
.
∴cos2α+cos2β+cos2γ=![]() =2.
=2.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
长方体ABCD-A1B1C1D1中,AB=3,BC=4,AA1=5 则三棱锥A1-ABC的体积为( )
| A、10 | B、20 | C、30 | D、35 |
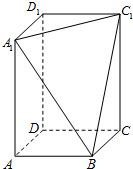 在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.
在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.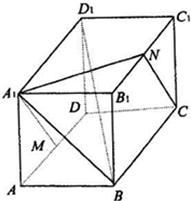 如图,长方体ABCD-A1B1C1D1中,AB=A1A=a,BC=
如图,长方体ABCD-A1B1C1D1中,AB=A1A=a,BC= 如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点.
如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点. 在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.
在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.