题目内容
若函数y=g(x)与y=x2+1(x≤0)互为反函数,则函数y=g(-x)大致图象为( )A.

B.

C.

D.

【答案】分析:先求出y=x2+1(x≤0)的反函数,再进一步求出函数y=g(-x)的解析式,判断出其定义域、值域,得到选项.
解答:解:y=x2+1(x≤0)的反函数为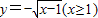 ,
,
即y=g(x)=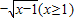 ,
,
所以y=g(-x)=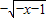 (x≤-1),
(x≤-1),
其值域为负值,
故选D.
点评:本题考查函数的反函数的求法,注意反函数的定义域为原函数的值域,值域为原函数的定义域,属于基础题.
解答:解:y=x2+1(x≤0)的反函数为
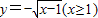 ,
,即y=g(x)=
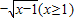 ,
,所以y=g(-x)=
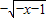 (x≤-1),
(x≤-1),其值域为负值,
故选D.
点评:本题考查函数的反函数的求法,注意反函数的定义域为原函数的值域,值域为原函数的定义域,属于基础题.

练习册系列答案
相关题目