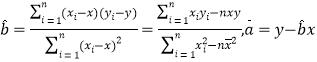题目内容
【题目】已知函数![]() (
(![]() )在同一半周期内的图象过点
)在同一半周期内的图象过点![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() 为坐标原点,
为坐标原点, ![]() 为函数
为函数![]() 图象的最高点,
图象的最高点, ![]() 为函数
为函数![]() 的图象与
的图象与![]() 轴的正半轴的交点,
轴的正半轴的交点, ![]() 为等腰直角三角形.
为等腰直角三角形.
(1)求![]() 的值;
的值;
(2)将![]() 绕原点
绕原点![]() 按逆时针方向旋转角
按逆时针方向旋转角![]() ,得到
,得到![]() ,若点
,若点![]() 恰好落在曲线
恰好落在曲线![]() (
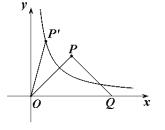
(![]() )上(如图所示),试判断点
)上(如图所示),试判断点![]() 是否也落在曲线
是否也落在曲线![]() (
(![]() )上,并说明理由.
)上,并说明理由.
【答案】(1)2;(2)见解析.
【解析】试题分析:(1)由已知利用周期公式可求最小正周期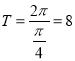 ,由题意可求Q坐标为(4,0).P坐标为(2,
,由题意可求Q坐标为(4,0).P坐标为(2, ![]() ),结合△OPQ为等腰直角三角形,即可得解
),结合△OPQ为等腰直角三角形,即可得解![]() ;
;
(2)由(Ⅰ)知, ![]() ,
, ![]() ,可求点P′,Q′的坐标,由点
,可求点P′,Q′的坐标,由点![]() 在曲线
在曲线![]() ,(x>0)上,利用倍角公式,诱导公式可求
,(x>0)上,利用倍角公式,诱导公式可求![]() ,又结合
,又结合![]() ,,可求
,,可求![]() 的值,由于
的值,由于![]() ,即可证明点Q′不落在曲线
,即可证明点Q′不落在曲线![]() (
(![]() )上.
)上.
试题解析:
(1)因为函数![]() (
(![]() )的最小正周期
)的最小正周期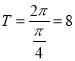 ,所以函数
,所以函数![]() 的半周期为
的半周期为![]() ,
,
所以![]() ,即有
,即有![]() 坐标为
坐标为![]() ,
,
又因为![]() 为函数
为函数![]() 图象的最高点,所以点
图象的最高点,所以点![]() 的坐标为
的坐标为![]() .
.
又因为![]() 为等腰直角三角形,所以
为等腰直角三角形,所以![]() .
.
(2)点![]() 不落在曲线
不落在曲线![]() (
(![]() )上,理由如下:
)上,理由如下:
由(1)知, ![]() ,
, ![]()
所以点![]() ,
, ![]() 的坐标分别为
的坐标分别为![]() ,
, ![]() .
.
因为点![]() 在曲线
在曲线![]() (
(![]() )上,所以
)上,所以![]() ,即
,即![]() ,又
,又![]() ,所以
,所以![]() .
.
又![]() .所以点
.所以点![]() 不落在曲线
不落在曲线![]() (
(![]() )上.
)上.

【题目】某电脑公司有6名产品推销员,其工作年限与推销金额数据如下表:
推销员编号 | 1 | 2 | 3 | 4 | 5 |
工作年限 | 3 | 5 | 6 | 7 | 9 |
推销金额 | 2 | 3 | 3 | 4 | 5 |
(1)求年推销金额![]() 关于工作年限
关于工作年限![]() 的线性回归方程;
的线性回归方程;
(2)若第6名推销员的工作年限为11年,试估计他的年推销金额.
附:线性回归方程![]() 中,
中, ,
,![]() ,其中
,其中![]() 为样本平均值.
为样本平均值.
【题目】某电脑公司有6名产品推销员,其工作年限与推销金额数据如下表:
推销员编号 | 1 | 2 | 3 | 4 | 5 |
工作年限 | 3 | 5 | 6 | 7 | 9 |
推销金额 | 2 | 3 | 3 | 4 | 5 |
(1)求年推销金额![]() 关于工作年限
关于工作年限![]() 的线性回归方程;
的线性回归方程;
(2)若第6名推销员的工作年限为11年,试估计他的年推销金额.
附:线性回归方程![]() 中,
中,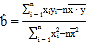 ,
,![]() ,其中
,其中![]() 为样本平均值.
为样本平均值.
【题目】中央电视台播出的《朗读者》节目,受到广大人民群众的喜爱.随着节目的播出,极大激发了观众对朗读以及经典的阅读学习积累的热情,从中获准匪浅,现从观看节目的观众中随机统计了4位观众的周均阅读学习经典的知识的时间(单位:小时)与年龄(单位:岁),并制作了对照表(如下表所示):
年龄 | 20 | 30 | 40 | 50 |
周均学习成语知识时间 | 2.5 | 3 | 4 | 4.5 |
由表中数据,试求线性回归方程![]() ,并预测年龄为50岁观众周均学习阅读经典知识的时间.
,并预测年龄为50岁观众周均学习阅读经典知识的时间.
参考公式: