题目内容
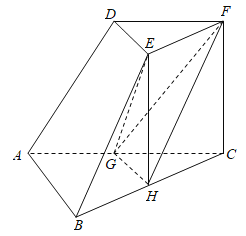
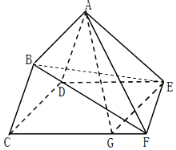
【题目】如图,在多面体ABCDEF中,四边形ABCD为平行四边形,平面ADE⊥平面CDEF,∠ADE=60°,DE∥CF,CD⊥DE,AD=2,DE=DC=3,CF=4,点G是棱CF上的动点.
(Ⅰ)当CG=3时,求证EG∥平面ABF;
(Ⅱ)求直线BE与平面ABCD所成角的正弦值;
(Ⅲ)若二面角G﹣AE﹣D所成角的余弦值为![]() ,求线段CG的长.
,求线段CG的长.
【答案】(Ⅰ)证明见详解;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]()
【解析】
(1)通过证明直线AB∥EG,从而由线线平行推证线面平行;
(2)过A作DE垂线AO,以![]() 为坐标原点,建立空间直角坐标系,求出平面的法向量以及直线的方向向量,从而求解线面角的正弦值;
为坐标原点,建立空间直角坐标系,求出平面的法向量以及直线的方向向量,从而求解线面角的正弦值;
(3)由(2)中所建的直角坐标系,根据二面角G﹣AE﹣D所成角的余弦值,求得G点的坐标,即可求得CG的长度.
(Ⅰ)证明:由已知得CG∥DE且CG=DE,
故四边形CDEG为平行四边形,
∴CD∥EG,
∵四边形ABCD为平行四边形,
∴CD∥AB,∴AB∥EG,
又EG平面ABF,AB平面ABF,
∴EG∥平面ABF.
(Ⅱ)过点A作AO⊥DE交DE于点O,过点O作OK∥CD交CF于点K
由(1)知平面ADE⊥平面CDEF,平面ADE∩平面CDEF=DE,AO平面ADE,
∴AO⊥平面CDEF,∵CD⊥DE,∴OK⊥DE,以O为原点建立如图的空间直角坐标系,
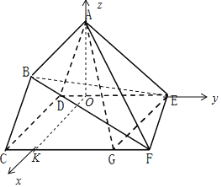
则D(0,﹣1,0),E(0,2,0),C(3,﹣1,0),
F(3,3,0),![]() ,D(0,﹣1,0),
,D(0,﹣1,0),
∴![]()
设平面ABCD的法向量为![]() ,
,
即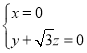 ,令z=﹣1,则
,令z=﹣1,则![]() ,
,
![]() ,
,
∴直线BE与平面ABCD所成角的正弦值为![]() ,
,
(Ⅲ)由题意得,G(3,4λ﹣1,0).
∴![]() ,
,
设平面AEG的法向量为![]() ,即
,即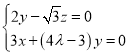 ,
,
令y=3,则![]() ,x=3﹣4λ,
,x=3﹣4λ,
∴![]() ,
,
容易得平面AED的法向量为![]() ,
,
故可得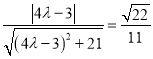 ,
,
解得![]() ,
,
∴![]() ,∴|CG|=λ|CF|=4λ
,∴|CG|=λ|CF|=4λ![]() ,
,
∵|CG|≤4,
∴![]() .
.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案