题目内容
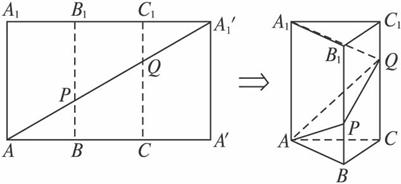
 如图,将长AA′=3
如图,将长AA′=3| 3 |
(1)求平面APQ与底面ABC所成二面角的正切值;
(2)求三棱锥A1-APQ的体积.
分析:(1)由题设知三棱柱ABC-A1B1C1 是正三棱柱,且侧棱AA1=3,底面边长为
,BP=1,CQ=2,由此能求出平面APQ与底面ABC所成二面角的正切值.
(2)连接A1P,由△A1AP的面积为
,知点Q到平面A1AP的距离为
,利用VA1-APQ=VQ-A1AP,能求出三棱锥A1-APQ的体积.
| 3 |
(2)连接A1P,由△A1AP的面积为
3
| ||
| 2 |
| 3 |
| 2 |
解答:解:(1)将长AA′=3
,宽AA1=3的矩形沿长的三等分线处折叠成一个三棱柱,
∴三棱柱ABC-A1B1C1 是正三棱柱,且侧棱AA1=3,
底面边长为
,BP=1,CQ=2,
延长QP交BC的延长线于点E,连接AE,
则AE⊥AC于A,QA⊥AE,
∴∠QAC为平面APQ与平面ABC所成的锐二面角的平面角,
∵AC=
,
∴tan∠QAC=
=
=
,
∴平面APQ与底面ABC所成二面角的正切值为
.
(2)连接A1P,
△A1AP的面积为
,点Q到平面A1AP的距离为
,
则VA1-APQ=VQ-A1AP=
×
×
=
.
| 3 |
∴三棱柱ABC-A1B1C1 是正三棱柱,且侧棱AA1=3,
底面边长为
| 3 |
延长QP交BC的延长线于点E,连接AE,
则AE⊥AC于A,QA⊥AE,
∴∠QAC为平面APQ与平面ABC所成的锐二面角的平面角,
∵AC=
| 3 |
∴tan∠QAC=
| QC |
| AC |
| 2 | ||
|
2
| ||
| 3 |
∴平面APQ与底面ABC所成二面角的正切值为
2
| ||
| 3 |
(2)连接A1P,
△A1AP的面积为
3
| ||
| 2 |
| 3 |
| 2 |
则VA1-APQ=VQ-A1AP=
| 1 |
| 2 |
| 3 |
| 2 |
3
| ||
| 2 |
3
| ||
| 4 |
点评:本题考查二面角的正切值的求法,考查棱锥的体积的求法.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
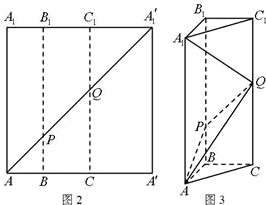 如图2所示,在边长为12的正方形AA'A'1A1中,点B,C在线段AA'上,且AB=3,BC=4,作BB1∥AA1,分别交A1A'1、AA'1于点B1、P,作CC1∥AA1,分别交A1A'1、AA'1于点C1、Q,将该正方形沿BB1、CC1折叠,使得A'A1′与AA1重合,构成如图3所示的三棱柱ABC-A1B1C1.
如图2所示,在边长为12的正方形AA'A'1A1中,点B,C在线段AA'上,且AB=3,BC=4,作BB1∥AA1,分别交A1A'1、AA'1于点B1、P,作CC1∥AA1,分别交A1A'1、AA'1于点C1、Q,将该正方形沿BB1、CC1折叠,使得A'A1′与AA1重合,构成如图3所示的三棱柱ABC-A1B1C1.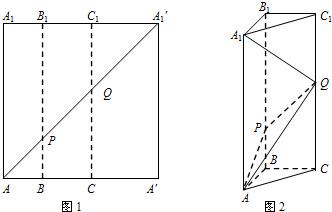 如图1所示,在边长为12的正方形AA′A1′A1中,点B,C在线段AA′上,且AB=3,BC=4,作BB1∥AA1,分别交A1A1′、AA1′于点B1、P,作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q,将该正方形沿BB1、CC1折叠,使得A′A1′与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1.
如图1所示,在边长为12的正方形AA′A1′A1中,点B,C在线段AA′上,且AB=3,BC=4,作BB1∥AA1,分别交A1A1′、AA1′于点B1、P,作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q,将该正方形沿BB1、CC1折叠,使得A′A1′与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1.