Question

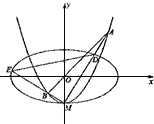
【题目】在平面直角坐标系中，已知两点， ，动点满足，线段的中垂线交线段于点.

（1）求点的轨迹的方程；

（2）过点的直线与轨迹相交于两点，设点，直线的斜率分别为，问是否为定值？并证明你的结论.

Answer 1

【答案】(1) ；(2)答案见解析.

【解析】试题分析：（1）利用椭圆定义求出点的轨迹的方程；

（2）讨论直线的斜率，当直线的斜率存在时，设直线的方程为，联立方程得，利用根与系数关系表示，即可得到定值.

试题解析：

（Ⅰ）以题意可得： ,，

所以点的轨迹是以为焦点，长轴长为的椭圆，

且

所以，

所以轨迹的方程为.

（Ⅱ）①当直线的斜率不存在时，由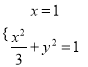，解得，

设， .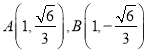

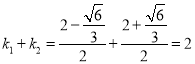②当直线的斜率存在时，设直线的方程为，

将代入整理化简，得，

依题意，直线与轨迹必相交于两点，设，

则， ，

又， ，

所以

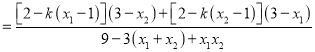
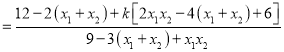
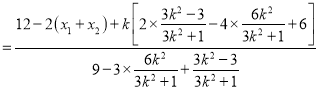
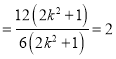
综上得： 为定值2.（说明：若假设直线为，按相应步骤给分）