题目内容
(2013•汕头二模)64个正数排成8行8列,如下所示: ,其中aij表示第i行第j列的数.已知每一行中的数依次都成等差数列,每一列中的数依次都成等比数列,且公比均为q,a11=
,其中aij表示第i行第j列的数.已知每一行中的数依次都成等差数列,每一列中的数依次都成等比数列,且公比均为q,a11=
,a24=1,a21=
.
(Ⅰ)求a12和a13的值;
(Ⅱ)记第n行各项之和为An(1≤n≤8),数列{an},{bn},{cn}满足an=
,mbn+1=2(an+mbn)(m为非零常数),cn=
,且
+
=100,求c1+c2+…+c7的取值范围;
(Ⅲ)对(Ⅱ)中的an,记dn=
(n∈N*),设Bn=d1d2…dn(n∈N*),求数列{Bn}中最大项的项数.
 ,其中aij表示第i行第j列的数.已知每一行中的数依次都成等差数列,每一列中的数依次都成等比数列,且公比均为q,a11=
,其中aij表示第i行第j列的数.已知每一行中的数依次都成等差数列,每一列中的数依次都成等比数列,且公比均为q,a11=| 1 |
| 2 |
| 1 |
| 4 |
(Ⅰ)求a12和a13的值;
(Ⅱ)记第n行各项之和为An(1≤n≤8),数列{an},{bn},{cn}满足an=
| 36 |
| An |
| bn |
| an |
| c | 2 1 |
| c | 2 7 |
(Ⅲ)对(Ⅱ)中的an,记dn=
| 200 |
| an |
分析:(Ⅰ)轻车熟路的公比,通过a11,a12,a13,a14成等差数列,求a12和a13的值;
(Ⅱ)设第一行公差为d,求出d,求出an=2n(1≤n≤8,n∈N*,推出
-
=
.说明{cn}是等差数列,推出-10
<c1+c7<10
.即可;
(Ⅲ)对(Ⅱ)中的an,记dn=
(n∈N*),设Bn=d1d2…dn(n∈N*),利用数列的单调性推出
,求出n即可求数列{Bn}中最大项的项数.
(Ⅱ)设第一行公差为d,求出d,求出an=2n(1≤n≤8,n∈N*,推出
| bn+1 |
| 2n+1 |
| bn |
| 2n |
| 1 |
| m |
| 2 |
| 2 |
(Ⅲ)对(Ⅱ)中的an,记dn=
| 200 |
| an |
|
解答:(共14分)
解:(Ⅰ)因为q=
=
,所以a14=
=2.
又a11,a12,a13,a14成等差数列,
所以a12=1,a13=
.…(4分)
(Ⅱ)设第一行公差为d,由已知得,a24=a14q=(
+3d)×
=1,
解得d=
.
所以a18=a11+7d=
+
=4.
因为an1=a11•(
)n-1=(
)n,an8=a18•(
)n-1=4×(
)n-1=8×(
)n.
所以An=
×8=36×(
)n,
所以an=2n(1≤n≤8,n∈N*).…(6分)
因为mbn+1=2(an+mbn),
所以mbn+1=2n+1+2mbn.
整理得
-
=
.
而cn=
,所以cn+1-cn=
,
所以{cn}是等差数列.…(8分)
故c1+c2+…+c7=
.
因为
≠0,
所以c1≠c7.
所以2c1c7<c12+c72.
所以(c1+c7)2=
+
+2c1c7<2(
+
)=200,
所以-10
<c1+c7<10
.
所以c1+c2+…+c7的取值范围是(-35
, 35
).…(10分)
(Ⅲ)因为dn=200×(
)n是一个正项递减数列,
所以当dn≥1时,Bn≥Bn-1,当dn<1时,Bn<Bn-1.(n∈N*,n>1)
所以{Bn}中最大项满足
即
…(12分)
解得6+log
<n≤7+log
.
又0<log
<1,且n∈N*,
所以n=7,即{Bn}中最大项的项数为7.…(14分)
解:(Ⅰ)因为q=
| a21 |
| a11 |
| 1 |
| 2 |
| a24 |
| q |
又a11,a12,a13,a14成等差数列,
所以a12=1,a13=
| 3 |
| 2 |
(Ⅱ)设第一行公差为d,由已知得,a24=a14q=(
| 1 |
| 2 |
| 1 |
| 2 |
解得d=
| 1 |
| 2 |
所以a18=a11+7d=
| 1 |
| 2 |
| 7 |
| 2 |
因为an1=a11•(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以An=
| an1+an8 |
| 2 |
| 1 |
| 2 |
所以an=2n(1≤n≤8,n∈N*).…(6分)
因为mbn+1=2(an+mbn),
所以mbn+1=2n+1+2mbn.
整理得
| bn+1 |
| 2n+1 |
| bn |
| 2n |
| 1 |
| m |
而cn=
| bn |
| an |
| 1 |
| m |
所以{cn}是等差数列.…(8分)
故c1+c2+…+c7=
| (c1+c7)×7 |
| 2 |
因为
| 1 |
| m |
所以c1≠c7.
所以2c1c7<c12+c72.
所以(c1+c7)2=
| c | 2 1 |
| c | 2 7 |
| c | 2 1 |
| c | 2 7 |
所以-10
| 2 |
| 2 |
所以c1+c2+…+c7的取值范围是(-35
| 2 |
| 2 |
(Ⅲ)因为dn=200×(
| 1 |
| 2 |
所以当dn≥1时,Bn≥Bn-1,当dn<1时,Bn<Bn-1.(n∈N*,n>1)
所以{Bn}中最大项满足
|
|
解得6+log
| 1 |
| 2 |
| 16 |
| 25 |
| 1 |
| 2 |
| 16 |
| 25 |
又0<log
| 1 |
| 2 |
| 16 |
| 25 |
所以n=7,即{Bn}中最大项的项数为7.…(14分)
点评:本题考查等差数列与等比数列的综合应用,函数的函数特征,考查分析问题解决问题的能力,数列的单调性的应用.

练习册系列答案
相关题目
 (2013•汕头二模)执行框图,若输出结果为
(2013•汕头二模)执行框图,若输出结果为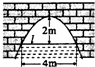 (2013•汕头二模)如图是抛物线形拱桥,当水面在l时,拱顶离水面2米,水面宽4米,水位下降2米后水面宽
(2013•汕头二模)如图是抛物线形拱桥,当水面在l时,拱顶离水面2米,水面宽4米,水位下降2米后水面宽