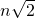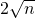题目内容
已知ai,bi∈R,(i=1,2,3,…,n),a12+a22+…+an2=1,b12+b22+…+bn2=1,则a1b1+a2b2+…+anbn的最大值为( )
A.n
| B.2
| C.2 | D.1 |
由题意,利用基本不等式得 a1b1+a2b2+…+anbn≤
+…+
=1
故选D
| ||||
| 2 |
| ||||
| 2 |
故选D

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目