题目内容
设△ABC的顶点A(1,3),边AB、AC上的中线所在直线的方程分别为x-2y+1=0,y=1,求△ABC中AB、AC各边所在直线的方程.
活动:为了搞清△ABC中各有关元素的位置状况,我们首先根据已知条件,画出图5,帮助思考问题.
解:如图8,设AC的中点为F,则AC边上的中线BF为y=1.
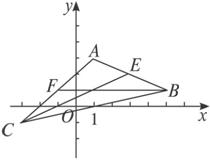
图8
AB边的中点为E,则AB边上中线CE为x-2y+1=0.
设C点坐标为(m,n).在A、C、F三点中A点已知,C点未知,F虽为未知但其在中线BF上,满足y=1这一条件.
这样用中点公式 解出n=-1.
解出n=-1.
又C点在中线CE上,应当满足CE的方程,则m-2n+1=0.
∴m=-3.∴C点为(-3,-1).
用同样的思路去求B点.设B点为(a,b),显然b=1.
又B点、A点、E点中,E为中点,B点为(a,1),
E点坐标为(![]() ,
,![]() ),即(
),即(![]() ,2).E点在CE上,应当满足CE的方程
,2).E点在CE上,应当满足CE的方程![]() -4+1=0,解出a=5.
-4+1=0,解出a=5.
∴B点为(5,1).
由两点式,即可得到AB,AC所在直线的方程.lAC:x-y+2=0.lAB:x+2y-7=0.
点评:此题思路较为复杂,应使同学们做完后从中领悟到两点:
(1)中点公式要灵活应用;
(2)如果一个点在直线上,则这点的坐标满足这条直线的方程,这一观念必须牢牢地树立起来.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目