题目内容
已知sin（θ+kπ）=-2cos（θ+kπ），k∈z．求值：
（1）
；
（2）9sin2θ-3sinθcosθ-5．
（1）
| 2sinθ-3cosθ | 4sinθ-9cosθ |
（2）9sin2θ-3sinθcosθ-5．
分析：（1）利用已知条件sin（θ+kπ）=-2cos（θ+kπ），k∈z求出tanθ=-2，将
分子、分母同除以cosθ，将tanθ的值代入即可．
（2）将9sin2θ-3sinθcosθ看成分母为1的分式形式，利用三角函数的平方关系将分母1用sin2θ+cos2θ代替，然后分子、分母同除以cos2θ，然后将tanθ的值代入即可．
| 2sinθ-3cosθ |
| 4sinθ-9cosθ |
（2）将9sin2θ-3sinθcosθ看成分母为1的分式形式，利用三角函数的平方关系将分母1用sin2θ+cos2θ代替，然后分子、分母同除以cos2θ，然后将tanθ的值代入即可．
解答：解：（1）由已知，tan（θ+kπ）=-2，
∵k∈z，进而tanθ=-2． …（2分）
∴
=
=
=
．…（6分）
（2）9sin2θ-3sinθcosθ-5=
-5=
-5=
．…（12分）
∵k∈z，进而tanθ=-2． …（2分）
∴
| 2sinθ-3cosθ |
| 4sinθ-9cosθ |
| 2tanθ-3 |
| 4tanθ-9 |
| 2×(-2)-3 |
| 4×(-2)-9 |
| 7 |
| 17 |
（2）9sin2θ-3sinθcosθ-5=
| 9sin2θ-3sinθcosθ |
| sin2θ+cos2θ |
| 9tan2θ-3tanθ |
| tan2θ+1 |
| 17 |
| 5 |
点评：已知条件是一个角的正切值，来求关于正弦、余弦的同次式子的值，一般讲分子、分母同除以余弦的最高次项，转化为关于正切的式子再求．
练习册系列答案
相关题目
；
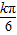，k∈{0，1，2，3，4，5，6，7，8，9，10，11}，其中使得sinα＜0的概率是（ ）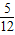
；
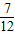