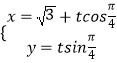题目内容
【题目】若f(x)＝x2－x＋b，且f(log2a)＝b，log2f(a)＝2(a>0且a≠1)．
（1）求a,b的值；
（2）求f(log2x)的最小值及相应x的值．
【答案】（1）2，2；（2）当
时，有最小值
【解析】
(1)
，再根据
，即可得到
，从而求出
，求出
,再根据
，即可求出
； (2)将
中的
换上
，即可得到
，进行配方即可求出的最小值及对应的值.
（1）∵f(x)＝x2－x＋b，∴f(log2a)＝(log2a)2－log2a＋b＝b，
∴log2a＝1，∴a＝2. 又∵log2f(a)＝2，∴f(a)＝4.
∴a2－a＋b＝4，∴b＝2.
（2）由（1）f(x)＝x2－x＋2.
∴f(log2x)＝(log2x)2－log2x＋2＝(log2x－
)2＋
.
∴当log2x＝，即x＝
时，f(log2x)有最小值.
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
