题目内容
三棱柱ABC-A1B1C1的底面为正三角形，且∠A1AB=∠A1AC，点A1到底面ABC的距离等于点A1到侧面B1BCC1的距离的2倍，则
=______．
| AA1 |
| AB |
作A1D⊥底面ABC于D，A1E⊥侧面B1BCC1于E，
∵∠A1AB=∠A1AC
∴D在∠BAC的平分线上，
又∵△ABC是正三角形，
∴AD⊥BC，又A1D⊥底面ABC，
∴AA1⊥BC，又AA1∥BB1，BB1⊥BC，
由题意得V=S△ABC•A1D=
BC2•2A1E=
S矩形B1BCC1•A1E=
BC•BB1•A1EA
∴
=
=
故答案为
∵∠A1AB=∠A1AC
∴D在∠BAC的平分线上，
又∵△ABC是正三角形，
∴AD⊥BC，又A1D⊥底面ABC，
∴AA1⊥BC，又AA1∥BB1，BB1⊥BC，
由题意得V=S△ABC•A1D=
| ||
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| BB1 |
| BC |
| AA1 |
| AB |
| 3 |
故答案为
| 3 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在三棱柱ABC-A1B1C1中，侧面AA1B1B是边长为2的正方形，点C在平面AA1B1B上的射影H恰好为A1B的中点，且CH=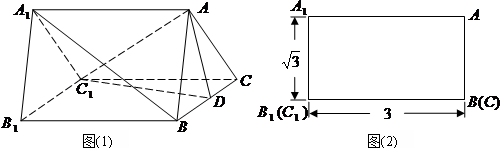
如图，在直三棱柱ABC-A1B1C1中，∠ACB=90°，∠BAC=30°，BC=1，
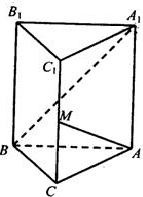
如图：在直三棱柱ABC-A1B1C1中，已知AB=A1A，AC=BC，点D、E分别为C1C、AB的中点，O为A1B与AB1的交点．