题目内容
已知双曲线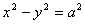 (其中
(其中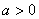 ).
).
(1)若定点 到双曲线上的点的最近距离为
到双曲线上的点的最近距离为 ,求
,求 的值;
的值;
(2)若过双曲线的左焦点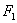 ,作倾斜角为
,作倾斜角为 的直线
的直线 交双曲线于
交双曲线于 、
、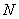 两点,其中
两点,其中 ,
, 是双曲线的右焦点.求△
是双曲线的右焦点.求△ 的面积
的面积 .
.
【答案】
(1)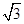 或
或 ;(2)
;(2)  .
.
【解析】
试题分析:(1)本题涉及两点间距离,因此我们设双曲线上任一点为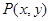 ,这样可表示出距离的平方
,这样可表示出距离的平方


 ,注意到双曲线上的点
,注意到双曲线上的点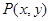 满足
满足 ,故要对
,故要对 进行分类讨论以求最小值;(2)设
进行分类讨论以求最小值;(2)设 ,
,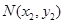 ,由于
,由于 ,因此
,因此 ,而
,而 可以用直线
可以用直线 方程与双曲线方程联立方程组,消去
方程与双曲线方程联立方程组,消去 可得
可得 的一元二次方程,从这个方程可得
的一元二次方程,从这个方程可得 ,从而得三角形面积.
,从而得三角形面积.
试题解析:(1)设点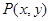 在双曲线上,由题意得:
在双曲线上,由题意得: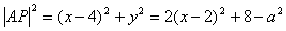 。
。
由双曲线的性质,得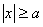 。 1分
。 1分
(i)若 ,则当
,则当 时,
时, 有最小值。最小值
有最小值。最小值 ,所以
,所以 。 3分
。 3分
(ii)若 ,则当
,则当 时,
时, 有最小值,此时
有最小值,此时 ,解得
,解得 。 6分
。 6分
(2) ,
,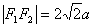 ,直线
,直线 与
与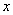 轴垂直时,
轴垂直时, ,此时,△
,此时,△ 的面积
的面积 =
=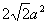 .
7分
.
7分
直线 与
与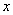 轴不垂直时,直线
轴不垂直时,直线 方程为
方程为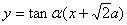 ,
8分
,
8分
设 ,
,
解法1:将 代入双曲线方程,整理得:
代入双曲线方程,整理得: ,即
,即
 10分
10分
所以,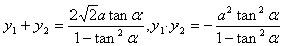 11分
11分

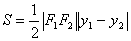
 =
= .
14分
.
14分
解法2:将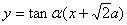 代入双曲线方程,整理得:
代入双曲线方程,整理得:
 ,
10分
,
10分
 ,
,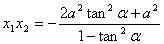 , 11分
, 11分

点 到直线
到直线 距离
距离 ,
,
△ 的面积
的面积
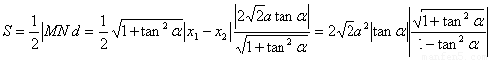
= .
14分
.
14分
考点:(1)定点到双曲线上点的最短距离;(2)直线与双曲线相交弦长及三角形面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知双曲线
已知双曲线