Question

【题目】已知函数的定义域为，且存在实常数，使得对于定义域内任意，都有成立，则称此函数具有“性质”

（1）判断函数是否具有“性质”，若具有“性质”，则求出的值；若不具有“性质”，请说明理由；

（2）已知函数具有“性质”且函数在上的最小值为；当时，，求函数在区间上的值域；

（3）已知函数既具有“性质”，又具有“性质”，且当时，，若函数，在恰好存在个零点，求的取值范围.

Answer 1

【答案】（1）具有，；（2）；（3）

【解析】

（1）假设函数具备性质，代入即可求出的值；

（2）根据题意可知，再根据函数的最小值即可求出值域；

（3）由题得且，作出图象，即可求出的取值范围．

解：（1）假设具有“性质”，

则恒成立，

等式两边平方整理得，，因为等式恒成立，

所以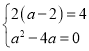，解得；

（2）函数具有“性质”则

又当时，，在单调递减

当时，得：，

又得

当时，，在单调递增

函数的最小值，得：

当时，，单调递减

此时的值域为：

（3）既具有“性质”，即，则函数为偶函数，

又既具有“性质”，即，

且当时，

作出函数的图象如图所示：

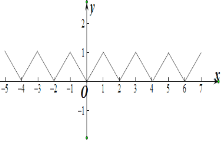
函数，在恰好存在个零点

与在恰好有个交点

且

即的取值范围为：.