题目内容
 已知圆心为O,半径为1,弧度数为π的圆弧
已知圆心为O,半径为1,弧度数为π的圆弧 |
| AB |
 |
| BC |
 |
| AC |
(1)若P为圆弧
 |
| BC |
| OP |
| OE |
(2)若E,F分别为线段OA,OC的中点,当P在圆弧
 |
| AB |
| PE |
| PF |
分析:(1)由题意可得C为
的中点,设OE=x(0≤x≤1),计算|
+
|2=(x-
)2+
,利用二次函数的性质求得它的最小值.
(2)以O为原点,BA所在的直线为x轴,建立平面直角坐标系,求出E、F的坐标,设P(x,y),则x2+y2=1(y≥0),计算
•
=(
-x,-y)•(-x,
-y)=1-
(x+y),可得当x+y取得最小值时,
•
取得最大值,计算求得结果.
 |
| AB |
| OP |
| OE |
| ||
| 2 |
| 1 |
| 2 |
(2)以O为原点,BA所在的直线为x轴,建立平面直角坐标系,求出E、F的坐标,设P(x,y),则x2+y2=1(y≥0),计算
| PE |
| PF |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| PE |
| PF |
解答:解:(1)由题意
=
可得 C为
的中点,设OE=x(0≤x≤1),
则 |
+
|2=
2+2
•
+
2= 1+2×1×x×cos
+x2=(x-
)2+
,
所以当x=
时,|
+
|的最小值为
.
(2)以O为原点,BA所在的直线为x轴,建立平面直角坐标系,则E(
,0),F(0,
),
设P(x,y),则x2+y2=1(y≥0),
∴
•
=(
-x,-y)•(-x,
-y)=1-
(x+y),
故当x=-1 且y=0时,x+y取得最小值为-1,所以,
•
的最大值是 1-(-
)=
.
 |
| BC |
 |
| AC |
 |
| AB |
则 |
| OP |
| OE |
| OP |
| OP |
| OE |
| OE |
| 3π |
| 4 |
| ||
| 2 |
| 1 |
| 2 |
所以当x=
| ||
| 2 |
| OP |
| OE |
| ||
| 2 |
(2)以O为原点,BA所在的直线为x轴,建立平面直角坐标系,则E(
| 1 |
| 2 |
| 1 |
| 2 |
设P(x,y),则x2+y2=1(y≥0),
∴
| PE |
| PF |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故当x=-1 且y=0时,x+y取得最小值为-1,所以,
| PE |
| PF |
| 1 |
| 2 |
| 3 |
| 2 |
点评:本题主要考查两个向量的数量积的定义,数量的坐标形式的运算,二次函数的性质应用,属于中档题.

练习册系列答案
相关题目
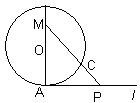 如图,已知圆心为O,半径为1的圆与直线l相切于点A,一动点P自切点A沿直线l向右移动时,取弧AC的长为
如图,已知圆心为O,半径为1的圆与直线l相切于点A,一动点P自切点A沿直线l向右移动时,取弧AC的长为 上有两点P,C,其中
上有两点P,C,其中 =
= (如图).
(如图). 的中点,E在线段OA上运动,求
的中点,E在线段OA上运动,求 的最小值;
的最小值; 上运动时,求
上运动时,求 的最大值.
的最大值.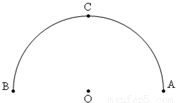
 上有两点P,C,其中
上有两点P,C,其中 =
= (如图).
(如图). 的中点,E在线段OA上运动,求
的中点,E在线段OA上运动,求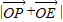 的最小值;
的最小值; 上运动时,求
上运动时,求 的最大值.
的最大值.