题目内容
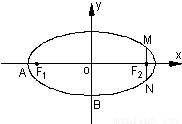
设椭圆C：
的左、右焦点分别为F1，F2，上顶点为A，过点A与AF2垂直的直线交x轴负半轴于点Q，且
，则椭圆C的离心率为
- A.
- B.
- C.
- D.
A
分析：设出Q的装备，结合向量条件及向量运算得出关于a，c的等式，从而求得椭圆的离心率．
解答：设Q（x0，0），由F2（c，0），A（0，b），则
=（-c，b），
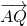=（x0，-b）
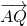∵⊥，∴-cx0-b2=0，∴x0=-
，
∵，∴F1为F2Q中点．
∴
∴b2=3c2=a2-c2，
∴椭圆的离心率e=
故选A．
点评：本题考查椭圆的离心率，考查向量知识的运用，确定关于a，c的等式是解题轭关键．
分析：设出Q的装备，结合向量条件及向量运算得出关于a，c的等式，从而求得椭圆的离心率．
解答：设Q（x0，0），由F2（c，0），A（0，b），则
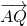=（-c，b），=（x0，-b）∵
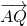⊥，∴-cx0-b2=0，∴x0=-，∵
，∴F1为F2Q中点．∴
∴b2=3c2=a2-c2，
∴椭圆的离心率e=
故选A．
点评：本题考查椭圆的离心率，考查向量知识的运用，确定关于a，c的等式是解题轭关键．
练习册系列答案
优学名师名题系列答案
相关题目
如图，在直角坐标系xOy中，已知椭圆C：
的离心率e＝
，左右两个焦分别为F1、F2．过右焦点F2且与x轴垂直的直线与椭圆C相交M、N两点，且|MN|＝1．
，(
)试求点P的轨迹方程，使点B关于该轨迹的对称点落在椭圆C上.
=1（a＞b＞0）的左、右两个焦 点。（1）若椭圆C上的点A（1，
）到F1、F2两点的 距离之和等于4，写出椭圆C的方程和焦点坐标；
+
=1（a＞b＞0）的离心率e=
，左右两个焦分别为F1、F2．过右焦点F2且与轴垂直的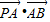
=m-4，（m∈R）试求点P的轨迹方程，使点B关于该轨迹的对称点落在椭圆C上．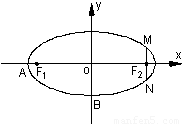
+
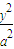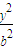=1（a＞b＞0）的离心率e=
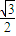，左右两个焦分别为F1、F2．过右焦点F2且与轴垂直的
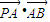=m-4，（m∈R）试求点P的轨迹方程，使点B关于该轨迹的对称点落在椭圆C上．