题目内容
已知双曲线与椭圆 有相同的焦距,它们离心率之和为
有相同的焦距,它们离心率之和为 ,则此双曲线的标准方程是 .
,则此双曲线的标准方程是 .
【答案】分析:首先由椭圆方程知其焦点在y轴上,并求出半焦距c与离心率e,然后设出双曲线的标准方程,并由它们离心率之和求出双曲线的离心率 ,进而求得a,再根据双曲线的性质b2=c2-a2求得b2,则问题解决.
,进而求得a,再根据双曲线的性质b2=c2-a2求得b2,则问题解决.
解答:解:由椭圆方程知其焦点在y轴上,且c= =4,e=
=4,e= ,
,
则设双曲线的标准方程为 ,
,
那么有 ,解得a=2,
,解得a=2,
所以b2=c2-a2=16-4=12,
因此双曲线的标准方程为 .
.
故答案为 .
.
点评:本题主要考查椭圆、双曲线的标准方程与性质.
 ,进而求得a,再根据双曲线的性质b2=c2-a2求得b2,则问题解决.
,进而求得a,再根据双曲线的性质b2=c2-a2求得b2,则问题解决.解答:解:由椭圆方程知其焦点在y轴上,且c=
 =4,e=
=4,e= ,
,则设双曲线的标准方程为
 ,
,那么有
 ,解得a=2,
,解得a=2,所以b2=c2-a2=16-4=12,
因此双曲线的标准方程为
 .
.故答案为
 .
.点评:本题主要考查椭圆、双曲线的标准方程与性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目




 有相同的焦点,且它们的离心率互为倒数,则该双曲线的方程为 .
有相同的焦点,且它们的离心率互为倒数,则该双曲线的方程为 . 与椭圆
与椭圆 有相同的焦点,点
有相同的焦点,点 、
、 分别是椭圆的右、右顶点,若椭圆经过点
分别是椭圆的右、右顶点,若椭圆经过点 .
. 是椭圆的右焦点,以
是椭圆的右焦点,以 为直径的圆记为
为直径的圆记为 ,过点
,过点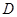 引圆
引圆 为直线
为直线 上的点,
上的点, 是圆
是圆 ,使得
,使得 ?若存在,求出定点
?若存在,求出定点 有相同的焦距,它们离心率之和为
有相同的焦距,它们离心率之和为 ,则此双曲线的标准方程是 .
,则此双曲线的标准方程是 .