题目内容
设函数f(x)= (a∈R)是R上的奇函数.
(a∈R)是R上的奇函数.
(Ⅰ)求a的值;
(Ⅱ)若m∈R+,且满足log >log3
>log3 ,求x的取值范围.
,求x的取值范围.
解:(Ⅰ)∵函数f(x)= ,f(-x)=
,f(-x)= =
= ,
,
根据f(x)为奇函数,∴f(-x)=-f(x),
即- =
= ,即 1+a•2x=-2x-a,解得 a=-1.
,即 1+a•2x=-2x-a,解得 a=-1.
(Ⅱ)由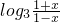 >log3
>log3 ,得
,得  ,
,
即 ,即
,即  .
.
当-1<1-m<1,即0<m<2时,1-m<x<1;
当1-m≤-1,即m≥2时,-1<x<1.
分析:(Ⅰ)根据函数f(x)求得f(-x),再由f(-x)=-f(x),求得a的值.
(Ⅱ)由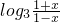 >log3
>log3 ,得
,得  ,
,
化简可得 .分-1<1-m<1,和当1-m≤-1两种情况,分别求得x的范围.
.分-1<1-m<1,和当1-m≤-1两种情况,分别求得x的范围.
点评:本题主要考查函数的奇偶性的应用,对数函数的单调性和特殊点,体现了转化、分类讨论的数学思想,
属于中档题.
 ,f(-x)=
,f(-x)= =
= ,
,根据f(x)为奇函数,∴f(-x)=-f(x),
即-
 =
= ,即 1+a•2x=-2x-a,解得 a=-1.
,即 1+a•2x=-2x-a,解得 a=-1. (Ⅱ)由
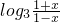 >log3
>log3 ,得
,得  ,
,即
 ,即
,即  .
. 当-1<1-m<1,即0<m<2时,1-m<x<1;
当1-m≤-1,即m≥2时,-1<x<1.
分析:(Ⅰ)根据函数f(x)求得f(-x),再由f(-x)=-f(x),求得a的值.
(Ⅱ)由
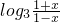 >log3
>log3 ,得
,得  ,
,化简可得
 .分-1<1-m<1,和当1-m≤-1两种情况,分别求得x的范围.
.分-1<1-m<1,和当1-m≤-1两种情况,分别求得x的范围.点评:本题主要考查函数的奇偶性的应用,对数函数的单调性和特殊点,体现了转化、分类讨论的数学思想,
属于中档题.

练习册系列答案
相关题目