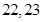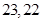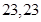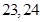题目内容
已知等差数列 中,
中,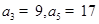 ,记数列
,记数列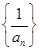 的前
的前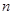 项和为
项和为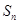 ,若
,若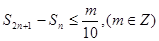 ,对任意的
,对任意的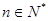 成立,则整数
成立,则整数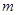 的最小值为
的最小值为
| A.5 | B.4 | C.3 | D.2 |
B
解析试题分析:因为等差数列中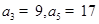 ,所以公差
,所以公差 ,
,
由 得,
得, ,
, ,
,
所以整数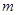 的最小值为4,选B。
的最小值为4,选B。
考点:本题主要考查等差数列的通项公式,放缩法。
点评:中档题,因为涉及数列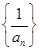 的前
的前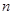 项和为
项和为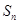 ,所以应从已知出发确定
,所以应从已知出发确定 的通项公式。探究过程中应用了“放缩法”。
的通项公式。探究过程中应用了“放缩法”。

练习册系列答案
相关题目
如果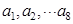 为各项都大于零的等差数列,公差
为各项都大于零的等差数列,公差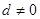 ,则
,则
A.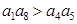 | B. |
C.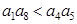 | D.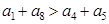 |
已知等差数列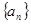 的前三项依次为
的前三项依次为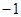 ,
, ,
,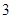 ,则此数列的通项公式为( )
,则此数列的通项公式为( )
A.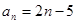 | B.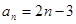 | C.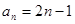 | D.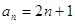 |
已知数列 ,
, ,
,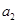 ,
, 成等差数列,
成等差数列,  ,
, ,
, ,
, ,
, 成等比数列,则
成等比数列,则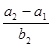 的值为( )
的值为( )
A. | B. | C. 或 或 | D. |
已知等差数列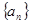 中,
中,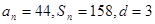 , 则n=( )
, 则n=( )
| A.4 | B.5 | C.6 | D.7 |
已知等差数列 的前
的前 项和为
项和为 ,则数列
,则数列 的前100项和为
的前100项和为
A. | B. | C. | D. |
若数列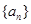 是等差数列,且
是等差数列,且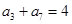 ,则数列
,则数列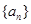 的前
的前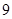 项和
项和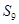 等于
等于
A.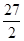 | B.18 | C.27 | D.36 |
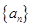 中,若a
中,若a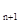 - a
- a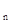
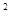 + a
+ a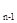 =0(n≥2),则S
=0(n≥2),则S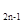 -4n=( )
-4n=( )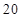 的样本数据,它们组成一个公差不为
的样本数据,它们组成一个公差不为 的等差数列
的等差数列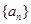 ,若
,若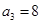 且前
且前 项和
项和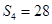 ,则此样本的平均数和中位数分别是
,则此样本的平均数和中位数分别是