题目内容

已知焦点在轴上的双曲线的两条渐近线过坐标原点，且两条渐近线与以

点 为圆心，1为半径的圆相切，又知的一个焦点与A关于直线对称．

（1）求双曲线的方程；

（2）设直线与双曲线的左支交于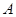，两点，另一直线经过 及的中点，求直线在轴上的截距的取值范围．

 

【答案】

（1）双曲线C的方程为:.

（2）

【解析】(1)设双曲线C的渐近线方程为,根据渐近线与圆相切，可得,求出k值，得到渐近线方程，可得a,b的一个等式关系，然后再利用焦点坐标可得c的值，得到另一个a,b的关系式，从而求出a,b的值.双曲线C的方程确定.

(2) 由得．

∵直线与双曲线左支交于两点，应满足，解得,

然后求出AB中点的坐标，从而得到直线l的方程为：．

令x=0可得b关于m的函数，从函数的角度研究b的取值范围

 

练习册系列答案
相关题目
（2013•潍坊一模）已知抛物线y2=2px（p＞0）的焦点F与双曲
x2
4
-
y2
5
=1的右焦点重合，抛物线的准线与x轴的交点为K，点A在抛物线上且|AK|=
2
|AF|，则A点的横坐标为（　　）
（2012•淮南二模）已知椭圆C：
x2
a2
+
y2
b2
=1，（a＞b＞0）与双曲4x2-
4
3
y2=1有相同的焦点，且椭C的离心e=
1
2
，又A，B为椭圆的左右顶点，M为椭圆上任一点（异于A，B）．
（1）求椭圆的方程；
（2）若直MA交直x=4于点P，过P作直线MB的垂线x轴于点Q，Q的坐标；
（3）求点P在直线MB上射R的轨迹方程．

（08年龙岩一中冲刺文）（分）已知双曲线C的中心在原点，焦点在x轴上，右准线为一条渐近线的方程是过双曲线C的右焦点F2的一条弦交双曲线右支于P、Q两点，R是弦PQ的中点.

   （1）求双曲线C的方程；

   （2）若A、B分别是双曲C上两条渐近线上的动点，且2|AB|=|F1F2|，求线段AB的中点M的迹方程，并说明该轨迹是什么曲线。

   （3）若在双曲线右准线L的左侧能作出直线m:x=a，使点R在直线m上的射影S满足，当点P在曲线C上运动时，求a的取值范围.

已知焦点在x轴上的双曲线C的两条渐近线过坐标原点，且两条渐近线与以点A (0，)为圆心，1为半径的圆相切，又知C的一个焦点与A关于y = x对称．

    （1）求双曲线C的方程；

    （2）若Q是双曲线线C上的任一点，F1，F2为双曲线C的左、右两个焦点，从F1引∠F1QF2的平分线的垂线，垂足为N，试求点N的轨迹方程；

    （3）设直线y = mx + 1与双曲线C的左支交于A、B两点，另一直线l经过M (–2，0)及AB的中点，求直线l在y轴上的截距b的取值范围．

已知抛物线的焦点F与双曲的右焦点重合，抛物线的准线与x轴的交点为K，点A在抛物线上且，则A点的横坐标为

A．            B．3                C．            D．4

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网