题目内容

已知定点A（2，0），动点P在抛物线y2=2x上运动，则|PA|的最小值为（　　）
A、4
B、3
C、2
D、
3
分析：设P（x，y）为抛物线上任一点，进而根据距离公式可得|PA|2=（x-2）2+y2利用x的范围求得|PA|的最小值即可．
解答：解：设P（x，y）为抛物线上任一点，
|PA|2=（x-2）2+y2=（x-2）2+2x=（x-1）2+3，
∵x∈[0，+∞），∴x=1时，|PA|min=
3
，
此时P（1，±
2
）．
故选D．
点评：本题主要考查抛物线的应用．综合了函数的定义域和值域的问题．
练习册系列答案
相关题目
已知定点A（-2，0），动点B是圆F：（x-2）2+y2=64（F为圆心）上一点，线段AB的垂直平分线交BF于P；
（1）求动点P的轨迹E的方程；
（2）直线y=
3
x+1与曲线E交于M，N两点，试问在曲线E位于第二象限部分上是否存在一点C，使
OM
+
ON
与
OC
共线（O为坐标原点）？若存在，求出点C的坐标；若不存在，请说明理由．
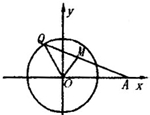精英家教网如图，已知定点A（2，0），点Q是圆x2+y2=1上的动点，∠AOQ的平分线交AQ于M，当Q点在圆上移动时，求动点M的轨迹方程．
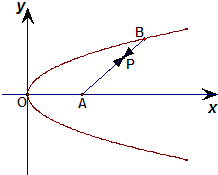如图，已知定点A（2，0）及抛物线y2=x，点B在该抛物线上，若动点P使得
AP
+2
BP
=
0
，求动点P的轨迹方程．
（2012•石家庄一模）在平面直角坐标系xOy中，已知定点A（-2，0）、B（2，0），M是动点，且直线MA与直线MB的斜率之积为-
1
4
，设动点M的轨迹为曲线C．
（I）求曲线C的方程；
（II ）过定点T（-1，0）的动直线l与曲线C交于P，Q两点，是否存在定点S（s，0），使得
SP
•
SQ
为定值，若存在求出s的值；若不存在请说明理由．
（2012•石家庄一模）在平面直角坐标系xOy中，已知定点A（-2，0）、B（2，0），M是动点，且直线MA与直线MB的斜率之积为-
1
4
，设动点M的轨迹为曲线C．
（I）求曲线C的方程；
（II）过定点T（-1，0）的动直线l与曲线C交于P，Q两点，若S（-
17
8
，0），证明：
SP
•
SQ
为定值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网