题目内容
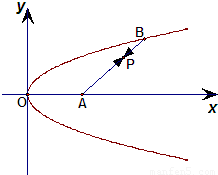
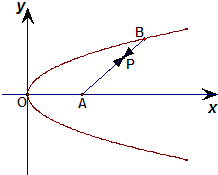 如图,已知定点A(2,0)及抛物线y2=x,点B在该抛物线上,若动点P使得
如图,已知定点A(2,0)及抛物线y2=x,点B在该抛物线上,若动点P使得| AP |
| BP |
| 0 |
分析:设动点的坐标为P(x,y),得到
,
的坐标表示,然后根据
+2
=
得出
求出B点的坐标,进而代入抛物线方程即可得答案.
| OP |
| AP |
| AP |
| BP |
| 0 |
| BP |
解答:解:设点P的坐标为(x,y),则
=(x,y),
=(x-2,y),
∵
+2
=
,
∴
=-
(x-2,y),
∴
=
+
=(x,y)+
(x-2,y)=(
x-1,
y),即点B坐标为(
x-1,
y),
而点B在抛物线y2=x上,因此有:(
y)2=
x-1,即y2=
(x-
).
∴动点P的轨迹方程为y2=
(x-
).
| OP |
| AP |
∵
| AP |
| BP |
| 0 |
∴
| BP |
| 1 |
| 2 |
∴
| OB |
| OP |
| PB |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
而点B在抛物线y2=x上,因此有:(
| 3 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
∴动点P的轨迹方程为y2=
| 2 |
| 3 |
| 2 |
| 3 |
点评:本题主要考查通过向量的有关运算求轨迹方程的问题.对向量的有关题型比如:求模、求夹角、求垂直以及平行等的问题一定要强化练习,是高考的热点问题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
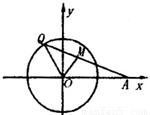
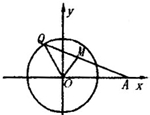 如图,已知定点A(2,0),点Q是圆x2+y2=1上的动点,∠AOQ的平分线交AQ于M,当Q点在圆上移动时,求动点M的轨迹方程.
如图,已知定点A(2,0),点Q是圆x2+y2=1上的动点,∠AOQ的平分线交AQ于M,当Q点在圆上移动时,求动点M的轨迹方程.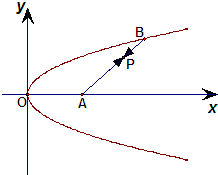 如图,已知定点A(2,0)及抛物线y2=x,点B在该抛物线上,若动点P使得
如图,已知定点A(2,0)及抛物线y2=x,点B在该抛物线上,若动点P使得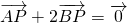 ,求动点P的轨迹方程.
,求动点P的轨迹方程.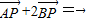 ,求动点P的轨迹方程.
,求动点P的轨迹方程.