题目内容
定义在 上的偶函数
上的偶函数 满足
满足 ,且在
,且在 上是减函数,
上是减函数, 是钝角三角形的两个锐角,则下列结论正确的是( )
是钝角三角形的两个锐角,则下列结论正确的是( )
A. B.
B.
C. D.
D.
【答案】
D
【解析】
试题分析:由 可知
可知 图象关于
图象关于
 对称,又因为
对称,又因为 为偶函数图象关于
为偶函数图象关于 对称,可得到
对称,可得到 为周期函数且最小正周期为2,结合
为周期函数且最小正周期为2,结合 在区间
在区间 上是减函数,画出满足题意的一个函数图象如右
上是减函数,画出满足题意的一个函数图象如右 图所示.因为
图所示.因为 是钝角三角形的两个锐角,所以
是钝角三角形的两个锐角,所以 ,
, ,所以
,所以 ,
,
所以 .
.
 ,故选D.
,故选D.
考点:函数的奇偶性、单调性
点评:本题主要考查了函数的奇偶性、单调性等综合应用,解决的关键一是由f(2-x)=f(x),偶函数满足的f(-x)=f(x)可得函数的周期,关键二是要熟练掌握偶函数对称区间上的单调性相反的性质,关键三是要α,β是钝角三角形的两个锐角可得0°<α+β<90°即0°<α<90°-β.本题是综合性较好的试题

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
 上的偶函数
上的偶函数 满足
满足 ,且在
,且在 上是增函数,下面是关于f(x)的判断
上是增函数,下面是关于f(x)的判断 :
: )对称 ②
)对称 ② 对称;
对称; .
. 上的偶函数满足:
上的偶函数满足: ,且当
,且当 时,
时, 单调递减,给出以下四个命题:①
单调递减,给出以下四个命题:① ;②
;② 是函数
是函数 上单调递增;④若方程
上单调递增;④若方程 .在区间
.在区间 上有两根为
上有两根为 ,则
,则 。以上命题正确的是 。(填序号)
。以上命题正确的是 。(填序号) 上的偶函数
上的偶函数 满足
满足 ,且在
,且在 上是减函数,
上是减函数, 是钝角三角形的两个锐角,则
是钝角三角形的两个锐角,则 与
与 的大小关系是
的大小关系是 B.
B.
 D.
D.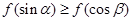
 上的偶函数
上的偶函数 满足
满足 对于
对于 恒成立,且
恒成立,且 ,则
,则 ___▲___.
___▲___. 上的偶函数
上的偶函数 满足:
满足: 且在区间
且在区间 上
上 性质的表述:
性质的表述: 的图象关于直线
的图象关于直线 对称; ②函数
对称; ②函数 是周期函数;
是周期函数; 时,
时, ; ④函数
; ④函数