题目内容
如图,已知立体图形ABCD—A1B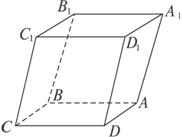
解析:证明BD⊥面AA
证明:如图,连结A
由四边形ABCD为菱形,得AC⊥BD,BC=CD.
又∠BCC1=∠DCC1,C
则△C1BC≌△C1DC,
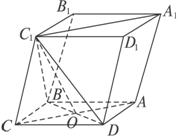
故C1B=C1D.
由于DO=OB,所以C1O⊥BD.
又∵AC⊥BD,AC∩C1O=O,
从而BD⊥平面AC1.
又C![]() 平面AC1,故C
平面AC1,故C
小结:证明线线垂直常用线面垂直来证明,也可以利用三垂线定理或逆定理证.

练习册系列答案
相关题目
题目内容
如图,已知立体图形ABCD—A1B
解析:证明BD⊥面AA
证明:如图,连结A
由四边形ABCD为菱形,得AC⊥BD,BC=CD.
又∠BCC1=∠DCC1,C
则△C1BC≌△C1DC,

故C1B=C1D.
由于DO=OB,所以C1O⊥BD.
又∵AC⊥BD,AC∩C1O=O,
从而BD⊥平面AC1.
又C![]() 平面AC1,故C
平面AC1,故C
小结:证明线线垂直常用线面垂直来证明,也可以利用三垂线定理或逆定理证.
