题目内容
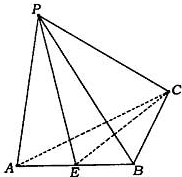 如图已知四面体P-ABC中,AB=BC=1,AC=
如图已知四面体P-ABC中,AB=BC=1,AC=| 2 |
| 3 |
| π |
| 4 |
(1)求点P在平面ABC内的射影到直线AB、AC的距离;
(2)求二面角P-EC-B的大小;
(3)求点B到平面PEC的距离.
分析:(1)首先可计算证得∠PAB=∠PCB=∠ABC=90°,设点P在平面ABC内的射影是点O,则OP=BP•sin
=
,根据PA⊥AB,PC⊥BC,可知OA⊥AB,OC⊥BC,从而OA、OC表示点O到直线AB、AC的距离,故可解;
(2)取BC的中点F,连接OF交CE于点G,正方形ABCO中,可知∠PGF为所求二面角的平面角,故可求二面角的大小;
(3)设OB交CE于点R,则OR=2BR,所以点O到平面PCE的距离等于点B到平面PCE的距离的2倍,过点O作直线OH垂直PG且相交于点H,则OH⊥平面PCE,从而可求点B到平面PEC的距离.
| π |
| 4 |
| 2 |
(2)取BC的中点F,连接OF交CE于点G,正方形ABCO中,可知∠PGF为所求二面角的平面角,故可求二面角的大小;
(3)设OB交CE于点R,则OR=2BR,所以点O到平面PCE的距离等于点B到平面PCE的距离的2倍,过点O作直线OH垂直PG且相交于点H,则OH⊥平面PCE,从而可求点B到平面PEC的距离.
解答: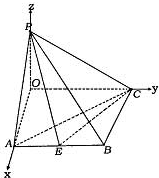 解:(1)由AB=BC=1,AC=
解:(1)由AB=BC=1,AC=
,PA=PC=
,PB=2
得到:∠PAB=∠PCB=∠ABC=90°
设点P在平面ABC内的射影是点O,
则OP=BP•sin
=
,…(2分)
由PA⊥AB,PC⊥BC得到,OA⊥AB,OC⊥BC,
且OA=OC=1,
所以点O到直线AB、AC的距离都是等于1;
(2)取BC的中点F,连接OF交CE于点G,正方形ABCO中,可以证明到OF⊥CE,所以∠PGF为所求二面角的平面角. …(6分)
∵CG=
=
⇒OG=
,∴tan∠PGO=
=
=
,
所以所求二面角的大小是π-arctan
…(8分)
(3)设OB交CE于点R,则OR=2BR,所以点O到平面PCE的距离等于点B到平面PCE的距离的2倍,
过点O作直线OH垂直PG且相交于点H,则OH⊥平面PCE,OH=
=
=
,
所以点B到平面PEC的距离是
.…(12分)
 解:(1)由AB=BC=1,AC=
解:(1)由AB=BC=1,AC=| 2 |
| 3 |
得到:∠PAB=∠PCB=∠ABC=90°
设点P在平面ABC内的射影是点O,
则OP=BP•sin
| π |
| 4 |
| 2 |
由PA⊥AB,PC⊥BC得到,OA⊥AB,OC⊥BC,
且OA=OC=1,
所以点O到直线AB、AC的距离都是等于1;
(2)取BC的中点F,连接OF交CE于点G,正方形ABCO中,可以证明到OF⊥CE,所以∠PGF为所求二面角的平面角. …(6分)
∵CG=
| OC•CF |
| OF |
| ||
| 5 |
2
| ||
| 5 |
| OP |
| OG |
| ||||
|
| ||
| 2 |
所以所求二面角的大小是π-arctan
| ||
| 2 |
(3)设OB交CE于点R,则OR=2BR,所以点O到平面PCE的距离等于点B到平面PCE的距离的2倍,
过点O作直线OH垂直PG且相交于点H,则OH⊥平面PCE,OH=
| OP•OG |
| PG |
| ||||||
|
2
| ||
| 7 |
所以点B到平面PEC的距离是
| ||
| 7 |
点评:本题以四面体为载体,考查点线距离,考查面面角,点面距离,考查学生分析转化问题的能力.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
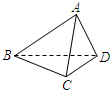 如图,已知正四面体ABCD的棱长为3cm.
如图,已知正四面体ABCD的棱长为3cm.



